Toán 10 Bài 23: Quy tắc đếm Toán 10 bài 23 Sách Kết nối tri thức

1 Đánh giá

Lý thuyết Toán 10 KNTT bài 23

1. Quy tắc cộng và sơ đồ hình cây
2. Quy tắc nhân
3. Kết hợp quy tắc cộng và quy tắc nhân

GiaiToan mời các bạn cùng tham khảo nội dung Toán 10 Bài 23: Quy tắc đếm nhằm ôn luyện, ghi nhớ và vận dụng kiến thức vào việc giải Toán 10 đạt kết quả cao.

1. Quy tắc cộng và sơ đồ hình cây

Quy tắc cộng

Giả sử một công việc nào đó có thể thực hiện theo một trong hai phương án khác nhau:

+ Phương án một có n1 cách thực hiện,

+ Phương án hai có n2 cách thực hiện.

(Phương án 1.......n1 cách

Phương án 2.......n2 cách)

Khi đó số cách thực hiện công việc sẽ là: ${n_1}\; + {\rm{ }}{n_2}$ cách.

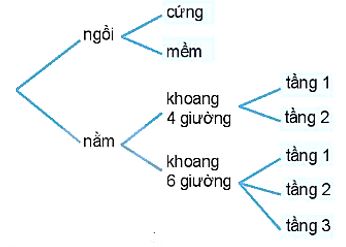
Chú ý: Sơ đồ minh hoạ cách phân chia trường hợp như trong hình bên dưới được gi là sơ đồ hình cây. Trong các bài toán đếm, người ta thường dùng sơ đỏ hình cây đề minh hoạ, giúp cho việc đếm thuận tiện và không bỏ sót trường hợp.

Toán 10 Bài 23: Quy tắc đếm

Ví dụ: Một quán phục vụ ăn sáng có bán phở và bún. Phở có 2 loại là phở bò và phở gà. Bún có 3 loại là bún bò, bún riêu cua và bún cá. Một khách hàng muốn chọn một món để ăn sáng. Vẽ sơ đỏ hỉnh cây minh hoạ và cho biết khách hàng đó có bao nhiêu cách lựa chọn một món ăn sáng.

Giải

Ta có sơ đỏ hình cây như hình sau

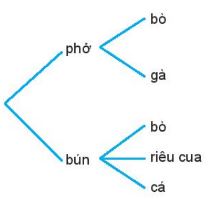
Toán 10 Bài 23: Quy tắc đếm

Theo quy tắc cộng, số cách chọn một món ăn sáng là:

2+3 = 5 (cách).

Chú ý: Ta áp dụng quy tắc công cho một công việc có nhiều phương án khi các phương án đó phải rời nhau, không phụ thuộc vào nhau (độc lập với nhau).

2. Quy tắc nhân

Quy tắc nhân

Giả sử một công việc nào đó phải hoàn thành qua hai công đoạn liên tiếp nhau:

+ Công đoạn một có m1 cách thực hiện,

+ Với mỗi cách thực hiện công đoạn một có m2 cách thực hiện công đoạn hai.

Khi đó số cách thực hiện công việc là: ${m_1}{\rm{.}}{{\rm{m}}_2}$ cách.

Chú ý

Quy tắc nhân áp dụng để tính số cách thực hiện một công việc có nhiều công đoạn, các công đoạn nối tiếp nhau và những công đoạn này độc lập với nhau.

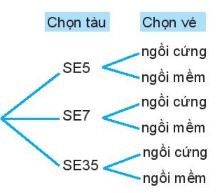
Ví dụ: Một người muốn mua vé tàu ngồi đi từ Hà Nội vào Vinh. Có ba chuyến tàu là SE5, SE7 và SE35. Trên mỗi tàu có 2 loại vé ngồi khác nhau: ngồi cứng hoặc ngồi mềm. Hỏi có bao nhiêu loại vé ngồi khác nhau để người đó lựa chọn?

Giải

Để mua được vé tàu, người đó phải thực hiện hai công đoạn:

Có 3 cách chọn chuyến tàu, với mỗi chuyến tàu có 2 cách chọn loại vé ngồi. Áp dụng quy tắc nhân, ta có số cách chọn loại vé là: 3 - 2 = 6 (cách).

Chú ý: Ta cũng có thể dùng quy tắc cộng. Người mua vé có thể lựa chọn một trong ba trường hợp: SE5, SE7 hoặc SE35.

Nếu lựa chọn SE5, có hai loại vé: loại vé SE5 ngồi cứng và SE5 ngồi mềm. Tương tự cho trường hợp SE7 và trường hợp SE35.

Mỗi trường hợp có hai loại vé. Tổng cộng có: 2+2+ 2= 6 (cách chọn loại vé).

Toán 10 Bài 23: Quy tắc đếm

3. Kết hợp quy tắc cộng và quy tắc nhân

Trong các ví dụ trước, chúng ta chỉ cần áp dụng một quy tắc đếm. Tuy nhiên, hầu hết các bài toán đếm trong thực tế sẽ phức tạp hơn và thường phải áp dụng cả hai quy tắc.

Ví dụ: Để tổ chức bữa tiệc, người ta chọn thực đơn gồm một món khai vị, một món chính và một món tráng miệng. Nhà hàng đưa ra danh sách: khai vị có 2 loại súp và 3 loại sa lát, món chính có 4 loại thịt, 3 loại cá và 3 loại tôm; tráng miệng có 5 loại kem và 3 loại bánh. Hỏi có thể thiết kế bao nhiêu thực đơn khác nhau?

Giải

Để chọn thực đơn, ta chia thành 3 công đoạn chọn món.

Công đoạn 1, chọn món khai vị: vì có hai phương án là súp hoặc sa lát nên ta áp dụng quy tắc cộng. Số cách chọn là: 2+ 3= 5 (cách).

Công đoạn 2, chọn món chính: tương tự, ta có số cách chọn là: 4+3: 3 = 10 (cách)

Công đoạn 3, chọn món tráng miệng: tương tự, ta có số cách chọn là: 5 + 3 = 8 (cách).

Tổng kết, theo quy tắc nhân, số cách chọn thực đơn là: 5 - 10 - 8 = 400 (cách).

Chú ý: Quy tắc cộng được áp dụng khi công việc được chia thành các phương án phân biệt (thực hiện một trong các phương án đẻ hoàn thành công việc).

Quy tắc nhân được áp dụng khi công việc có nhiều công đoạn nói tiếp nhau (phải thực hiện tất cả các công đoạn để hoàn thành công việc).

Toán 10 Bài 23: Quy tắc đếm được giáo viên GiaiToan tổng hợp và đăng tải nhằm hy vọng với phần lý thuyết này sẽ giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tham khảo thêm các bài lý thuyết khác được đăng tải chi tiết bám sát chương trình học SGK Kết nối tri thức với cuộc sống tại Lý thuyết Toán 10 đồng thời tại chuyên mục Giải Toán 10 Kết nối tri thức Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn tập nhé.