Toán 10 bài 15: Hàm số Toán 10 bài 15 Sách Kết nối tri thức

2 Đánh giá

Toán 10 KNTT bài 15

1. Khái niệm hàm số
2. Đồ thị của hàm số
3. Sự đồng biến, nghịch biến của hàm số

Lý thuyết Toán 10 KNTT bài 15 - Hàm số được GiaiToan đăng tải dưới đây là phần tóm tắt kiến thức trọng tâm nhằm hỗ trợ các bạn ôn luyện và nắm vững kĩ năng học tốt môn Toán lớp 10.

1. Khái niệm hàm số

Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Lý thuyết Toán 10 KNTT bài 15

Ví dụ: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vảo thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5s, 10s.

Giải

Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S (mét) phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t lả biến số, S = S(t) là hàm số của t.

Tập xác định của hàm số là Ð= [0; +).

Quảng đường vật đi được sau 5s là: S1 = S(5) = 2.5 = 10 (m).

Quảng đường vật đi được sau 10s là: S2 = S(10) = 2.10 = 20 (m).

Chú ý: Khi cho hàm số bằng công thức y= f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

2. Đồ thị của hàm số

Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ với mọi x thuộc D.

Ví dụ: Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số này.

Giải

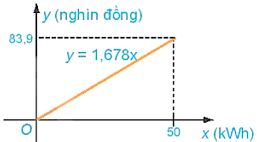
Lý thuyết Toán 10 KNTT bài 15

Công thức của hàm số cho ở HĐ3b là y = 1,678x với $0 \le x \le 50$ .

Tập xác định của hàm số này là D = [0: 50]

Vì $0 \le x \le 50 nên 0 \le y \le 1,678.50 = 83,9$ .

Vậy tập giá trị của hàm số là [0; 83,9].

Đỏ thị của hàm số y = 1,678x trên [0; 50] là một đoạn thẳng.

3. Sự đồng biến, nghịch biến của hàm số

Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu

$\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$ .

Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu

$\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$ .

Ví dụ: Hàm số y = x² đồng biến hay nghịch biến trên mỗi khoảng $\left( { - \infty ;0} \right)$ và $\left( {0; + \infty } \right)$ ?

Giải

Vẽ đồ thị hàm số y= f{x) = x² như hình sau:

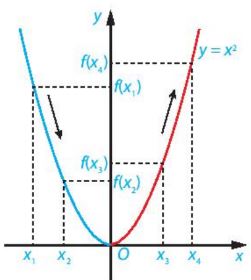
Lý thuyết Toán 10 KNTT bài 15

+ Trên khoảng $\left( { - \infty ;0} \right)$ , đồ thị “đi xuống" từ trái sang phải và với ${x_1},{x_2} \in \left( { - \infty ;0} \right), {x_1} < {x_2}$ thì $f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$ . Như vậy hàm số y = x² nghịch biến trên khoảng $\left( { - \infty ;0} \right)$ .

+ Trên khoảng $\left( {0; + \infty } \right)$ , đồ thị "đi lên” từ trái sang phải và với ${x_3},{x_4} \in \left( {0; + \infty } \right), {x_3} < {x_4} thì f\left( {{x_3}} \right) < f\left( {{x_4}} \right)$ . Như vậy, hàm số y = x² đồng biến trên khoảng $\left( {0; + \infty } \right)$ .

Chú ý

+ Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

+ Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường "đi xuống" từ trái sang phải.

Lý thuyết Toán 10 KNTT bài 15: Hàm số được giáo viên GiaiToan tổng hợp và đăng tải nhằm hy vọng với phần lý thuyết này sẽ giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tham khảo thêm các bài lý thuyết khác được đăng tải chi tiết bám sát chương trình học SGK Kết nối tri thức với cuộc sống tại Lý thuyết Toán 10 đồng thời tại chuyên mục Giải Toán 10 Kết nối tri thức Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn tập nhé.