Luyện tập 3 trang 51 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

1 Đánh giá

Luyện tập 3 trang 51 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan sưu tầm và đăng tải. Hướng dẫn các em trả lời câu hỏi trong bài, giúp các em ôn tập, củng cố kiến thức Toán lớp 10. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Luyện tập 3 trang 51 Toán 10 Tập 1

Đề bài:

Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:

$a)\ {x^2} + 2x + 2 > 0$

$b)\ - 3{x^2} + 2x - 1 > 0$

Phương pháp giải:

Bước 1: Vẽ đồ thị biểu diễn các hàm số.

Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.

Lời giải chi tiết:

a) Ta có đồ thị:

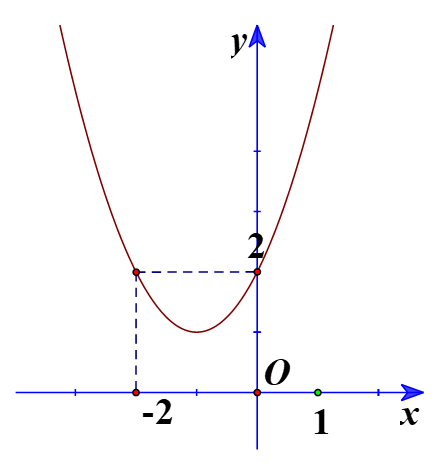
Luyện tập 3 trang 51 Toán 10 Tập 1

Từ đồ thị ta thấy ${x^2} + 2x + 2 > 0$ biểu diễn phần parabol $y = {x^2} + 2x + 2$ nằm phía trên trục hoành, tương ứng với mọi $x \in \mathbb{R}$ .

Vậy tập nghiệm của bất phương trình ${x^2} + 2x + 2 > 0$ là $\mathbb{R}$ .

b) Ta có đồ thị:

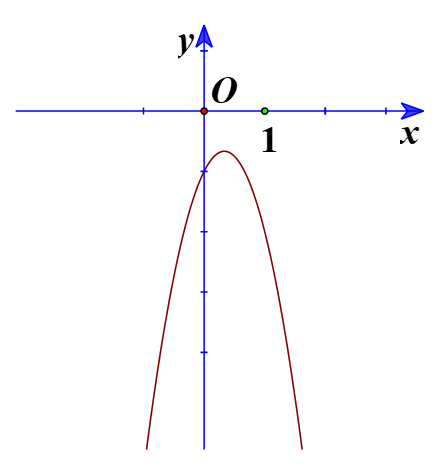
Luyện tập 3 trang 51 Toán 10 Tập 1

Từ đồ thị ta thấy $- 3{x^2} + 2x - 1 > 0$ biểu diễn phần parabol $y = - 3{x^2} + 2x - 1$ nằm phía trên trục hoành, tương ứng với $x \in \emptyset$

Vậy tập nghiệm của bất phương trình $- 3{x^2} + 2x - 1 > 0$ là $\emptyset$ .

>> Bài tiếp theo: Luyện tập 4 trang 53 Toán 10 Tập 1 SGK Cánh Diều

Luyện tập 3 trang 51 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, củng cố kiến thức cũng như chuẩn bị tốt cho các bài kiểm tra Toán lớp 10 sắp tới. Chúc các em học tốt ngoài ra các em có thể tham khảo thêm các dạng bài tập Toán lớp 10 do GiaiToan giải và biên tập nhé.

Chia sẻ bởi: