Toán 10 Bài 25: Nhị thức Newton Toán 10 bài 25 Sách Kết nối tri thức

1 Đánh giá

Toán 10 Bài 25: Nhị thức Newton được GiaiToan tổng hợp và đăng tải trong bài viết dưới đây, mời các bạn cùng tham khảo.

Lý thuyết Toán 10 KNTT bài 25

Các tích nhận được từ sơ đồ hình cây của một tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Hơn nữa, tổng của chúng cho ta khai triển của tích các đa thức đã cho.

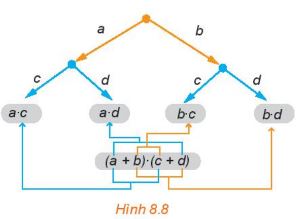
Chẳng hạn, trong sơ đỏ hình cây (H.8.8) của (a + b)(c + d) thì các tích nhận được là a.c, a.d, b.c, b.d cũng chính là các tích nhận được khi ta lấy một hạng tử của nhị thức thứ nhất (là a hoặc b) nhân với một hạng tử của nhị thức thứ hai (là c hoặc d). Ta có

$\left( {a + b} \right).\left( {c + d} \right) = a.c + a.d + b.c + b.d$

Toán 10 Bài 25: Nhị thức Newton

Ta có công thức sau:

$\begin{array}{l} {\left( {a + b} \right)^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}. \end{array}$

Toán 10 Bài 25: Nhị thức Newton

Ví dụ: Khai triển ${\left( {2x + 1} \right)^4}$ .

Giải

Thay a = 2x và b = 1 trong công thức khai triển của ${\left( {a + b} \right)^4}$ , ta được:

$\begin{array}{l} {\left( {2x + 1} \right)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}.1 + 6.{\left( {2x} \right)^2}{.1^2} + 4.\left( {2x} \right){.1^3} + {1^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 16{x^4} + 32{x^3} + 24{x^2} + 8x + 1 \end{array}$

Ta có công thức sau:

$\begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array}$

Toán 10 Bài 25: Nhị thức Newton

Ví dụ: Khai triển ${\left( {x + 3} \right)^5}$ .

Giải

Thay a = x và b = 3 trong công thức khai triển của ${\left( {a + b} \right)^5}$ , ta được:

$\begin{array}{*{20}{l}} {{{\left( {x + 3} \right)}^5} = {x^5} + 5.{x^4}.3 + 10.{x^3}{{.3}^2} + 10.{x^2}{{.3}^3} + 5.x{{.3}^4} + {3^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x^5} + 15{x^4} + 90{x^3} + 270{x^2} + 405x + 243.} \end{array}$

Nhận xét: Các công thức khai triển ${\left( {a + b} \right)^n} với n \in \left\{ {4;5} \right\}$ , là một công cụ hiệu quả để tính chính xác hoặc xấp xỉ một số đại lượng mà không cần dùng máy tính.

Toán 10 Bài 25: Nhị thức Newton do GiaiToan tổng hợp và đăng tải nhằm hy vọng với phần lý thuyết này sẽ giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tham khảo thêm các bài lý thuyết khác được đăng tải chi tiết bám sát chương trình học SGK Kết nối tri thức với cuộc sống tại Lý thuyết Toán 10 đồng thời tại chuyên mục Giải Toán 10 Kết nối tri thức Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn tập nhé.