Giaitoan.com Toán 12

Tìm m để hàm số có 7 cực trị Cực trị của hàm số

Nội dung
  • 5 Đánh giá

Tìm m để hàm số có cực trị

Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, GiaiToan.com xin mời quý thầy cô và các bạn học sinh tham khảo tài liệu Tìm tham số m để hàm số có 7 cực trị. Bộ tài liệu giới thiệu đến bạn đọc các phương pháp giải bài tập ứng dụng tìm tham số m để hàm số có cực trị cùng hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.

Tìm m để hàm số có 7 điểm cực trị

Ví dụ 1: Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới:

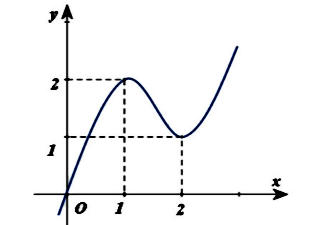
Tìm m để hàm số có 7 cực trị

Số giá trị nguyên của tham số m trong đoạn [-100; 100] để hàm số h(x) = |f2(|x|) + 2f(|x|)– m| có đúng 7 cực trị là:

A. 97

B. 95

C. 96

D. 98

Hướng dẫn giải

Đặt g(x) = f2(|x|) + 2f(|x|)– m

=> g’(x) = 2f(|x|).f’(|x|.\frac{x}{{\left| x \right|}} + 2f’(x).\frac{x}{{\left| x \right|}} = 2.\frac{x}{{\left| x \right|}}.f’(|x|).(f(|x|) + 1)

g’(x) = 0

=> \left[ {\begin{array}{*{20}{c}} {f'\left( {\left| x \right|} \right) = 0} \\ {f'\left( {\left| x \right|} \right) = - 1\left( L \right)} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \pm 1} \\ {x = \pm 2} \end{array}} \right.

g’(x) không xác định tại x = 0

Ta có bảng biến thiên như sau:

Tìm m để hàm số có 7 cực trị

Từ bảng biến thiên suy ra hàm số h(x) = |g(x)| có đúng 7 điểm cực trị

\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {8 - m \leqslant 0} \\ {\left\{ {\begin{array}{*{20}{c}} {3 - m \geqslant 0} \\ { - m < 0} \end{array}} \right.} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m \geqslant 8} \\ {0 < m \leqslant 3} \end{array}} \right.

Mà m ∈ [-100; 100]

=> m ∈ {1; 2; 3; 8; 9; …; 100}

Vậy có 96 giá trị của m thỏa mãn điều kiện đề bài.

Chọn đáp án C

Ví dụ 2: Tổng tất cả các giá trị nguyên của tham số m để hàm số y = |3x2 – 4x3 – 12x2 + 3m| có 7 điểm cực trị bằng

A. 2

B. 5

C. 3

D. 1

Hướng dẫn giải

Xét hàm số y = f(x) = 3x2 – 4x3 – 12x2 + 3m

Tập xác định

Có y’ = 12x3 – 12x2 – 24x

y’ = 0

<=> x = 0 hoặc x = -1 hoặc x = 2

Ta có bảng biến thiên như sau:

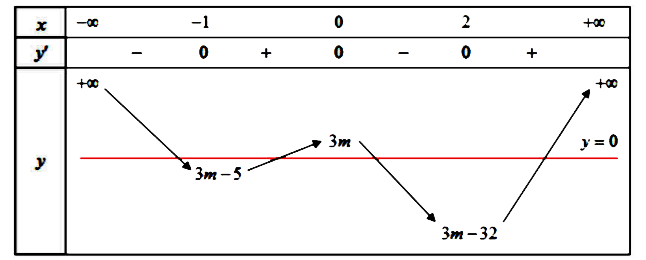
Tìm m để hàm số có 7 cực trị

Từ bảng biến thiên ta thấy

Hàm số y = f(x) có 3 điểm cực trị

Khi đó hàm số y = |f(x)| có 7 điểm cực trị khi phương trình f(x) = 0 có 4 nghiệm phân biệt bội lẻ

=> \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {3m - 5 < 0} \\ {3m > 0} \end{array}} \right. \Leftrightarrow 0 < m < \frac{5}{3}

Mà m là số nguyên

=> m = 1

Vậy tổng các giá trị nguyên của m thỏa mãn điểu kiện đề bài bằng 1

Chọn đáp án D

---------------------------------------------------------------

Trên đây GiaiToan đã giới thiệu đến thầy cô và học sinh tài liệu Tìm tham số m để hàm số thỏa mãn điều kiện, hy vọng tài liệu sẽ là công cụ hữu ích giúp học sinh ôn thi THPT Quốc gia hiệu quả.

Một số tài liệu liên quan:

Chia sẻ bởi: Bờm
Mời bạn đánh giá!
  • Lượt xem: 5.587
Tìm thêm: Toán 12 ôn thi thpt quốc gia 2021
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần