Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Bài 1.23 trang 32 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 4

Nội dung
  • 1 Đánh giá

Bài 1.23 trang 32 Toán 12 KNTT

Toán 12 Bài 1.23 trang 32 Tập 1 là câu hỏi trong bài Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số với lời giải chi tiết giúp cho các em học sinh tham khảo, củng cố kỹ năng giải Toán 12 Kết nối tri thức.

Giải Bài 1.23 Toán 12 trang 32

Bài 1.23 trang 32 toán 12 tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) y = \frac{2x^{2} -x+4}{x-1}

b) y = \frac{x^{2} +2x+1}{x+3}

Lời giải chi tiết:

a) y = \frac{2x^{2} -x+4}{x-1}

1. Tập xác định của hàm số: \mathbb{R} \setminus \left \{ 1 \right \}

2. Sự biến thiên: Viết y= 2x+1+\frac{5}{x-1}

  • Ta có: y'=2-\frac{5}{\left(x-1\right)^2} = \frac{2x^2-4x+3}{\left(x-1\right)^2}

Vậy y'=0 \Leftrightarrow \frac{2x^2-4x+3}{\left(x-1\right)^2} =0\Leftrightarrow x=\frac{2+\sqrt{10} }{ 2} hoặc x=\frac{2-\sqrt{10} }{ 2}

  • Trên các khoảng \left(-\infty;\frac{2-\sqrt{10}}{2}\right) và \left(\frac{2+\sqrt{10}}{2}; +\infty \right),y' > 0 nên hàm số đồng biến trên từng khoảng này.

Trên các khoảng \left( \frac{2-\sqrt{10}}{2} ; 1\right) và \left(1;\frac{2+\sqrt{10}}{2} \right) , y' < 0 nên hàm số nghịch biến trên từng khoảng này.

  • Hàm số đạt cực đại tại x=\frac{2-\sqrt{10} }{ 2} với y_{CĐ}=3-2\sqrt{10}

Hàm số đạt cực tiểu tại x=\frac{2+\sqrt{10} }{ 2} với y_{CT}=3 + 2\sqrt{10}

  • \lim_{x\rightarrow - \infty} y =\lim_{x\rightarrow - \infty} \frac{2x^{2} -x+4}{x-1} =\lim_{x\rightarrow - \infty} \frac{2x -1 +\frac{ 4}{x } }{1-\frac{1}{x } }= - \infty

\lim_{x\rightarrow + \infty} y =\lim_{x\rightarrow + \infty} \frac{2x^{2} -x+4}{x-1} =\lim_{x\rightarrow + \infty} \frac{2x -1 +\frac{ 4}{x } }{1-\frac{1}{x } }= + \infty

  • Tiệm cận: \lim_{x\rightarrow 1^-} y = \lim_{x\rightarrow 1^-} \left ( 2x+1+\frac{5}{x-1} \right )= - \infty

\lim_{x\rightarrow 1^+} y = \lim_{x\rightarrow 1^+} \left ( 2x+1+\frac{5}{x-1} \right )= + \infty

\lim_{x\rightarrow + \infty} [y -(2x+1)] = \lim_{x\rightarrow + \infty} \left ( \frac{5}{x-1} \right )= 0

\lim_{x\rightarrow -\infty} [y -(2x+1)] = \lim_{x\rightarrow - \infty} \left ( \frac{5}{x-1} \right )= 0

Do đó, đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1 và tiệm cận xiên là đường thẳng y = 2x + 1

  • Bảng biến thiên:

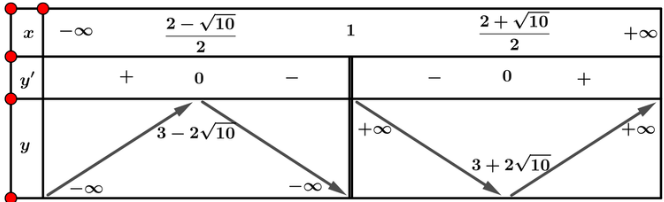
3. Đồ thị:

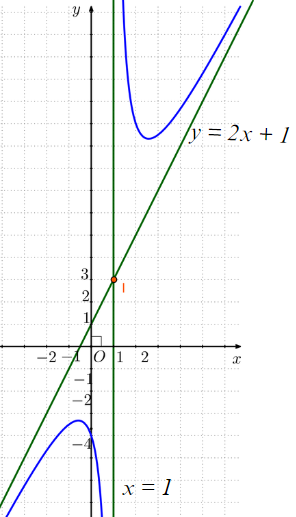
Giao điểm của đồ thị hàm số với trục tung là điểm (0; - 4).

Điểm (2; 10) thuộc đồ thị của hàm số.

Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

b) y = \frac{x^{2} +2x+1}{x+3}

Đang cập nhật...

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 28
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

Chủ đề liên quan

Mới nhất trong tuần