Giaitoan.com Toán 9

Đề khảo sát chất lượng đầu năm môn Toán 9 Đề 1 Đề thi khảo sát lớp 9

Nội dung Tải về
  • 11 Đánh giá

Đề khảo sát chất lượng đầu năm lớp 9 môn Toán - Có đáp án

Đề thi khảo sát chất lượng đầu năm Toán lớp 9 năm học 2022 - 2023 được GiaiToan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 8 giúp học sinh ôn tập, củng cố kiến thức đã được học trong chương trình Toán tiểu học. Đây là nền tảng vững chắc giúp các bạn học sinh nắm chắc kiến thức Toán lớp 8 để chuẩn bị nền tảng kiến thức vững chắc bước vào năm học lớp 9 sắp tới. Mời các bạn cùng tham khảo chi tiết.

Đề tham khảo liên quan: Đề khảo sát chất lượng đầu năm môn Toán 9 Đề 2

A. Đề thi khảo sát chất lượng đầu năm môn Toán 9 Đề 1

PHÒNG GD&ĐT ……..

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

Bài 1: (1,5 điểm) Cho biểu thức: A = \left( {\frac{1}{{x - 2}} + \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{x + 2}}} \right).\left( {\frac{2}{x} - 1} \right)

a, Rút gọn biểu thức A.

b, Tìm x để A = 1

Bài 2: (2,5 điểm) Giải các phương trình và bất phương trình sau:

a) |2x - 1| + x = 14

b) \frac{{2x + 2}}{3} < 2 + \frac{{x - 2}}{2}

c) \frac{3}{{x + 1}} - \frac{2}{{x - 2}} = \frac{{4x - 2}}{{\left( {x + 1} \right)\left( {x - 2} \right)}}

Bài 3: (1,5 điểm) Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được \frac{2}{3} quãng đường bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết rằng thời gian bạn ấy đi từ nhà đến trường là 28 phút.

Bài 4: (3 điểm) Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm, đường phân giác AD. Đường vuông góc với DC cắt AC ở E.

a) Chứng minh rằng tam giác ABC và tam giác DEC đồng dạng.

b) Tính độ dài các đoạn thẳng BC, BD.

c) Tính độ dài AD.

d) Tính diện tích tam giác ABC và diện tích tứ giác ABDE.

Bài 5: (0,5 điểm) Một hình lăng trụ đứng có đáy là tam giác vuông được minh họa bằng hình vẽ dưới đây:

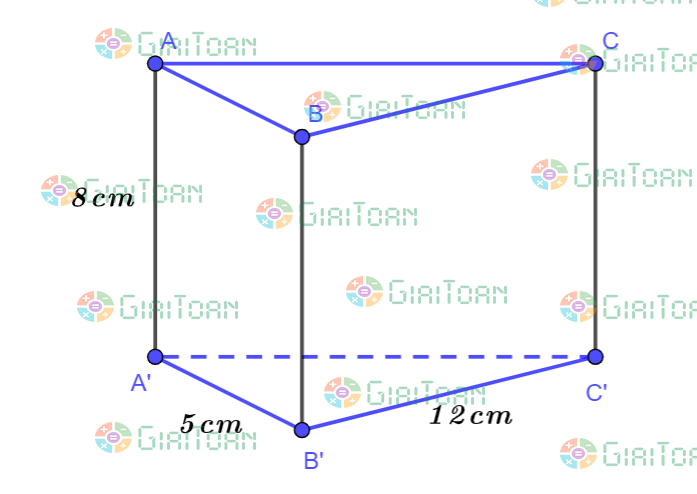
Đề khảo sát chất lượng đầu năm môn Toán 9 Đề 1

Độ dài hai cạnh góc vuông của đáy là 5cm, 12cm, chiều cao của lăng trụ là 8cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.

Bài 6: (1 điểm) Cho phương trình ẩn x sau: \left( {2x + m} \right)\left( {x - 1} \right) + mx + m = 2{x^2} + 2. Tìm các giá trị của m để phương trình có nghiệm là một số không âm.

B. Đáp án đề khảo sát chất lượng đầu năm môn Toán 9 – Đề 1

Bài 1:

a) A = \left( {\frac{1}{{x - 2}} + \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{x + 2}}} \right).\left( {\frac{2}{x} - 1} \right)

Điều kiện xác định: x \ne \pm 2;x \ne 0

\begin{matrix} A = \left( {\dfrac{1}{{x - 2}} + \dfrac{{2x}}{{{x^2} - 4}} + \dfrac{1}{{x + 2}}} \right).\left( {\dfrac{2}{x} - 1} \right) \hfill \\ A = \dfrac{{x + 2 + 2x + x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\left( {\dfrac{{2 - x}}{x}} \right) \hfill \\ A = \dfrac{{4x}}{{x + 2}}.\dfrac{{ - 1}}{x} = \dfrac{{ - 4}}{{x + 2}} \hfill \\ \end{matrix}

b) Điều kiện xác định: x \ne \pm 2;x \ne 0

A = 1 \Rightarrow \frac{{ - 4}}{{x + 2}} = 1 \Leftrightarrow x + 2 = - 4 \Leftrightarrow x = - 6 (thỏa mãn điều kiện)

Vậy x = -6 thì A có giá trị bằng 1

Bài 2:

a) |2x - 1| + x = 14

Nếu 2x - 1 \geqslant 0 \Rightarrow x \geqslant \frac{1}{2}

=> |2x – 1| = 2x – 1

Phương trình tương đương

2x – 1 + x = 14

=> 3x = 15

=> x = 5 (thỏa mãn điều kiện)

Nếu 2x - 1 < 0 \Rightarrow x < \frac{1}{2}

=> |2x – 1| = - 2x + 1

Phương trình tương đương

- 2x + 1 + x = 14

=>-x = 13

=> x = -13 (thỏa mãn điều kiện)

Vậy phương trình có nghiệm x = 5 hoặc x = 13

b) \frac{{2x + 2}}{3} < 2 + \frac{{x - 2}}{2}

=> 2(2x + 2) < 12 + 3(x – 2)

=> 4x + 4 < 12 + 3x – 6

=> 4x – 3x < 12 – 6 – 4

=> x < 2

Vậy bất phương trình có nghiệm x < 2

c) \frac{3}{{x + 1}} - \frac{2}{{x - 2}} = \frac{{4x - 2}}{{\left( {x + 1} \right)\left( {x - 2} \right)}}

Điều kiện xác định: x \ne 2;x \ne 1

=> \frac{{3\left( {x - 2} \right) - 2\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{{4x - 2}}{{\left( {x + 1} \right)\left( {x - 2} \right)}}

=> 3x – 6 – 2x – 2 = 4x – 2

=> 3x – 2x – 4x = -2 + 6 +2

=> -3x = 6

=> x = - 2 (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình là S = {-2}

Bài 3:

Gọi quãng đường cần tìm là x (km). Điều kiện x > 0

Quãng đường đi với vận tốc 4km/h là \frac{2}{3}x (km)

=> Thời gian đi là \frac{2}{3}x:4 = \frac{x}{6} (giờ)

Quãng đường đi với vận tốc 5km/h là \frac{1}{3}x (km)

=> Thời gian đi là \frac{1}{3}x:5 = \frac{x}{{15}} (giờ)

Thời gian đi hêt quãng đường là 28 phút tương ứng với \frac{7}{{15}} giờ

Ta có phương trình: \frac{x}{6} + \frac{x}{{15}} = \frac{7}{{15}} \Rightarrow x = 2

(thỏa mãn điều kiện)\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}

Vậy quãng đường từ nhà đến trường của bạn học sinh đó là 2km.

Bài 4:

Xét tam giác ABC và tam giác DEC ta có:

\widehat {BAC} = \widehat {EDC} = {90^0}

Góc C chung

Tính được BC = 5 cm

+ Áp dụng tính chất đường phân giác ta có: \frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}

+ Áp dụng tính chất dãy tỉ số bằng nhau ta có: \frac{{DB}}{3} = \frac{{DC}}{4} = \frac{{DB + DC}}{{3 + 4}} = \frac{{BC}}{7} = \frac{5}{7}

+ Tính được DB = \frac{{15}}{7}cm

Dựng DH ⊥ AB => DH // AC (Do cùng vuông góc với AB)

\Rightarrow \frac{{DH}}{{AC}} = \frac{{BD}}{{BC}} \Rightarrow DH = \frac{{\frac{{15}}{7} \cdot 4}}{5} = \frac{{12}}{7}(Hệ quả định lý Ta lét)

Chứng minh tam giác AHD vuông cân và tính được DA = \sqrt {\frac{{288}}{{49}}}

{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}3.4 = 6(c{m^2})

Tính DE = \frac{{15}}{7}cm

{S_{DCE}} = \frac{{150}}{{49}}c{m^2}

\Rightarrow {S_{ABDE}} = {S_{ABC}} - {S_{DCE}} = \frac{{144}}{{49}}c{m^2}

Bài 5:

- Tính cạnh huyền của đáy: \sqrt {{5^2} + {{12}^2}} = 13 (cm)

- Diện tích xung quanh của lăng trụ:

(5 + 12 + 13). 8 = 240 (cm2)

- Diện tích một đáy:

(5.12) : 2 = 30 (cm2)

- Thể tích lăng trụ: 30.8 = 240(cm3)

Bài 6:

(2x + m)(x – 1) – 2x2 + mx + m – 2 = 0

=> 2x2 - 2x + mx – m - 2x2 + mx + m - 2 = 0

=> (m - 1).x = 1

Để phương trình có nghiệm là một số không âm thì m - 1 > 0

=> m > 1

Vậy m > 1 thì phương trình có nghiệm là một số không âm.

Mời quý thầy cô và học sinh tải tài liệu tham khảo đầy đủ!

---------------------------------------

Trên đây GiaiToan.com đã giới thiệu Đề thi khảo sát chất lượng đầu năm môn Toán 9. Mời các bạn học sinh tham khảo thêm các tài liệu học tập lớp 8 hay như Giải Toán 9, đề thi học kì 1 Toán 9, đề thi học kì 2 Toán 9, ....được cập nhật liên tục trên GiaiToan.com.

Tham khảo thêm:

Đề thi thử vào lớp 10 năm 2022 môn Toán

Chia sẻ bởi: Bắp
Mời bạn đánh giá!
  • Lượt tải: 801
  • Lượt xem: 27.667
  • Dung lượng: 412,2 KB
Tìm thêm: Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần