Giaitoan.com Toán 9 Luyện tập Toán 9

Từ điểm M ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến Giải Toán 9

Nội dung
  • 2 Đánh giá

Chứng minh tứ giác nội tiếp

Bài tập Toán 9: Tứ giác nội tiếp được GiaiToan.com biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các bạn học sinh ngoài bài tập trong sách giáo khoa (sgk) có thể luyện tập thêm các dạng bài tập cơ bản và nâng cao Toán hình lớp 9. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán 9 và ôn tập thi vào lớp 10. Mời các bạn học sinh và quý thầy cô cùng tham khảo tài liệu chi tiết!

Bài toán: Từ điểm M ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến MA, MB của (O) (với A, B là các tiếp điểm) và cát tuyến MDE không qua tâm O (D, E thuộc (O), D nằm giữa M và E).

a) Chứng minh Tứ giác AMBO nội tiếp

b) Gọi H là giao điểm của OM và AB. Chứng minh OM vuông góc với AB và MD.ME = MA2

c) Gọi S là giao điểm của ED và AB. Chứng minh: MD.SE = ME.SD

Lời giải chi tiết

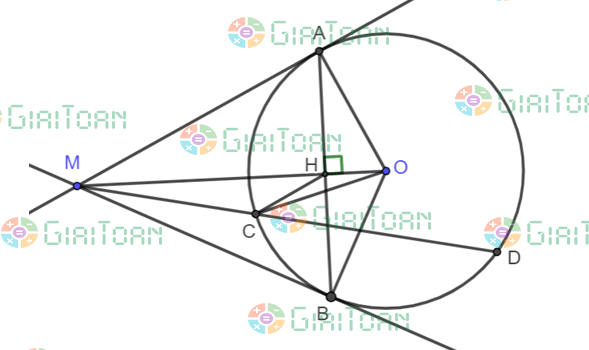
Từ điểm M ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến

a) Vì MA và MB là tiếp tuyến của (O)

=> \widehat {MAO} = \widehat {MBO} = {90^0}

=> \widehat {MAO} + \widehat {MBO} = {180^0}

=> Tứ giác MAON nội tiếp đường tròn

b) Xét tam giác MBC và tam giác MBD có:

\widehat {BMD} là góc chung

\begin{matrix} \widehat {CBM} = \widehat {BDM} \hfill \\ \Rightarrow \Delta MBC \sim MDB\left( {g - g} \right) \hfill \\ \Rightarrow \dfrac{{BM}}{{DM}} = \dfrac{{CM}}{{BM}} \hfill \\ \Rightarrow M{B^2} = MC.MD\left( * \right) \hfill \\ \end{matrix}

c) Xét tam giác MOB ta có:

\begin{matrix} \widehat B = {90^0} \hfill \\ BH \bot MO \hfill \\ \end{matrix}

=> MB2 = MH . MO (**)

Từ (*) và (**) suy ra MC . MD = MH . MO

Xét tam giác MHC và tam giác MOD có:

\widehat {DMO} là góc chung

\begin{matrix} \dfrac{{MC}}{{OM}} = \dfrac{{HM}}{{DM}} \hfill \\ \Rightarrow \Delta MCH \sim MOD\left( {c - g - c} \right) \hfill \\ \Rightarrow \widehat {MHC} = \widehat {ODM}\left( 1 \right) \hfill \\ \end{matrix}

=> Tứ giác OHCD nội tiếp đường tròn

=> \widehat {DHO} = \widehat {DCO}

Mặt khác \widehat {MDO} = \widehat {DCO} \Rightarrow \widehat {OHD} = \widehat {MDO}\left( 2 \right)

Từ (1) và (2) suy ra \widehat {MHC} = \widehat {OHD} \Rightarrow \widehat {CHB} = \widehat {DHB}

=> AD là phân giác của góc DHC

---------------------------------------------

Tài liệu liên quan:

Hy vọng tài liệu Chuyên đề Toán 9: Tứ giác nội tiếp giúp sẽ giúp ích cho các bạn học sinh học nắm chắc cách giải các bài tập hình học nâng cao đồng thời học tốt môn Toán lớp 9 ôn thi vào 10. Chúc các bạn học tốt, mời các bạn tham khảo! Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 9, Lý thuyết Toán 9, Giải Toán 9, Luyện tập Toán 9, ...

Chia sẻ bởi: Người Nhện
Mời bạn đánh giá!
  • Lượt xem: 3.515
Tìm thêm: Chuyên đề Toán 9 Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần