Giaitoan.com Toán 9 Luyện tập Toán 9

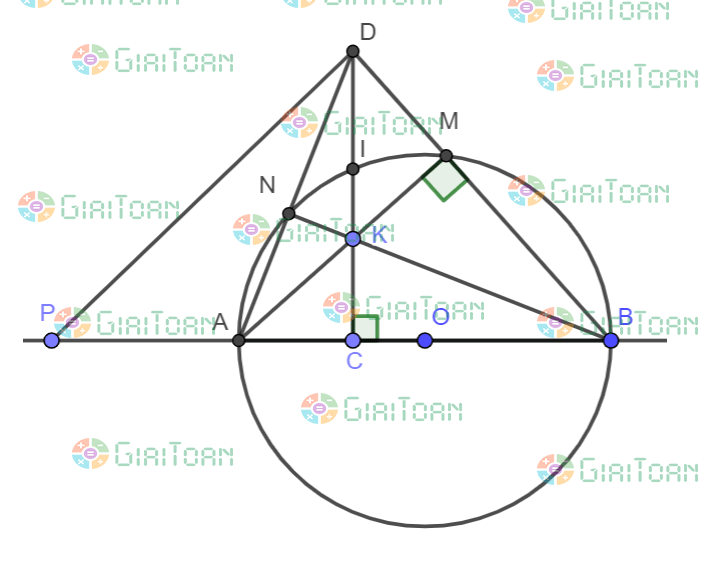
Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K Giải Toán 9

Nội dung
  • 10 Đánh giá

Chứng minh tứ giác nội tiếp

Bài tập Toán 9: Tứ giác nội tiếp được GiaiToan.com biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các bạn học sinh ngoài bài tập trong sách giáo khoa (sgk) có thể luyện tập thêm các dạng bài tập cơ bản và nâng cao Toán hình lớp 9. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán 9 và ôn tập thi vào lớp 10. Mời các bạn học sinh và quý thầy cô cùng tham khảo tài liệu chi tiết!

Bài toán: Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D.Chứng minh:a) Các tứ giác ACMD, BCKM nội tiếp đường trònb) CK.CD = CA.CBc) Gọi N là giao điểm của AD và đường tròn O chứng minh B, K, N thẳng hàngd) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI

Lời giải chi tiết

Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K

a) Theo bài ra ta có:

AB là đường kính của đường tròn tâm O

=> AM \bot MB  (tính chất)

=> \widehat {DMA} = \widehat {DCA} = {90^0}

=> Tứ giác ACMD nội tiếp đường tròn.

Ta lại có: \widehat {BCK} = \widehat {BMK} = {90^0}

=> Tứ giác BCKM nội tiếp đường tròn.

b) Xét tam giác CKA và tam giác CBD ta có:

\begin{matrix} \widehat {BCK} = \widehat {BMK} = {90^0} \hfill \\ \widehat {KAC} = \widehat {MAC} = \widehat {MDC} = \widehat {BDC} \hfill \\ \Rightarrow \Delta CAK \sim \Delta CDB\left( {g - g} \right) \hfill \\ \Rightarrow \dfrac{{AC}}{{DC}} = \dfrac{{KC}}{{BC}} \hfill \\ \end{matrix}

=> KC . DC = AC . BC

c) Ta có: N thuộc (O)

=> AN \bot BN = > BN \bot AD

Do AM \bot BD;BN \bot AD,AM \cap BN = \left\{ K \right\} nên K là trực tâm tam giác DAB

=> BK \bot AD

Vậy ba điểm B, K, N thẳng hàng

d) Trên tia đối của tia CB lấy điểm P sao cho CP = CB

Ta có: KC . DC = AC . BC (chứng minh câu b)

\Rightarrow \frac{{KC}}{{AC}} = \frac{{CE}}{{CD}}

Do \widehat {ACK} = \widehat {ECD} \Rightarrow \Delta CAK \sim \Delta CDE\left( {c - g - c} \right)

\Rightarrow \widehat {AKC} = \widehat {DEA}

=> Tứ giác AKDE nội tiếp đường tròn

=> Điểm P thuộc tam giác AKD

=> Tâm đường tròn ngoại tiếp tam giác AKD nằm trên trung trực AP cố định.

Tứ giác nội tiếp là gì?

- Tứ giác nội tiếp đường tròn là tứ giác có bôn đỉnh nằm trên một đường tròn. Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.

Cách chứng minh tứ giác nội tiếp

Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm

Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)

Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.

Tham khảo tài liệu tại đây: Hướng dẫn phương pháp chứng minh tứ giác nội tiếp

---------------------------------------------

Tài liệu liên quan:

------------------------------------------------

Hy vọng tài liệu Chuyên đề Toán 9: Tứ giác nội tiếp giúp sẽ giúp ích cho các bạn học sinh học nắm chắc cách giải các bài tập hình học nâng cao đồng thời học tốt môn Toán lớp 9 ôn thi vào 10. Chúc các bạn học tốt, mời các bạn tham khảo! Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 9, Lý thuyết Toán 9, Giải Toán 9, Luyện tập Toán 9, ...

Chia sẻ bởi: Bọ Cạp
Mời bạn đánh giá!
  • Lượt xem: 28.268
Tìm thêm: Chuyên đề Toán 9 Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần