Giaitoan.com Hỏi bài Hỏi đáp Toán 10
thich game1123 Hỏi đáp Toán 10 Toán 10 bài tập Toán 10

Tìm giá trị của tham số m để:-4 < (2x^2+mx-4)/(-x^2+x-1) < 6 với mọi x thuộc R

Tìm giá trị của tham số m để:

-4 < (2x^2+mx-4)/(-x^2+x-1) < 6 với mọi x thuộc R

3
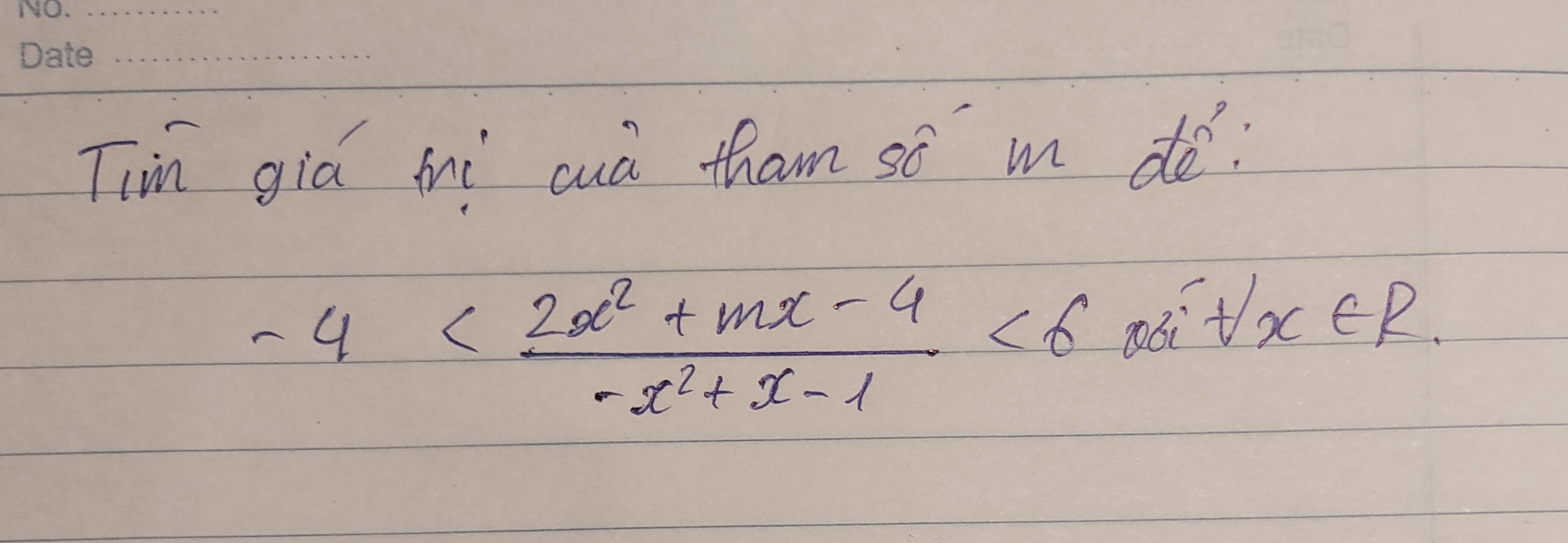
Xóa Đăng nhập để viết
3 Câu trả lời
  • Captain
    Captain

    Hướng dẫn giải

    Điểu kiện xác định - {x^2} + x - 1 \leqslant \frac{{ - 3}}{4},\forall x \in \mathbb{R}

    \begin{matrix} \frac{{2{x^2} + mx - 4}}{{ - {x^2} + x - 1}} < 6 \hfill \\ \Rightarrow \frac{{2{x^2} + mx - 4}}{{ - {x^2} + x - 1}} - \frac{{6\left( { - {x^2} + x - 1} \right)}}{{ - {x^2} + x - 1}} < 0 \hfill \\ \Rightarrow \frac{{2{x^2} + mx - 4 + 6{x^2} - 6x + 6}}{{ - {x^2} + x - 1}} < 0 \hfill \\ \Rightarrow \frac{{8{x^2} + mx - 6x + 2}}{{ - {x^2} + x - 1}} < 0\left( * \right) \hfill \\ \end{matrix}

    Do - {x^2} + x - 1 \leqslant \frac{{ - 3}}{4},\forall x \in \mathbb{R}

    => 8x2 + mx – 6x +2 > 0 với mọi x thuộc R

    => Δ < 0

    => (m – 6)2 – 4.8.2 < 0

    => m2 – 12m – 28 <0

    => m ∈ (-2; 14) (điều 1)

    \begin{matrix} \frac{{2{x^2} + mx - 4}}{{ - {x^2} + x - 1}} > - 4 \hfill \\ \Rightarrow \frac{{2{x^2} + mx - 4}}{{ - {x^2} + x - 1}} + \frac{{4\left( { - {x^2} + x - 1} \right)}}{{ - {x^2} + x - 1}} > 0 \hfill \\ \Rightarrow \frac{{2{x^2} + mx - 4 - 4{x^2} + 4x - 4}}{{ - {x^2} + x - 1}} > 0 \hfill \\ \Rightarrow \frac{{ - 2{x^2} + mx + 4x - 8}}{{ - {x^2} + x - 1}} > 0\left( {**} \right) \hfill \\ \end{matrix}

    Do - {x^2} + x - 1 \leqslant \frac{{ - 3}}{4},\forall x \in \mathbb{R}

    => -2x2 + mx + 4x – 8 < 0 với mọi x thuộc R

    => Δ < 0

    => (m + 4)2 + 4.2.8 < 0

    => m2 + 8m + 80 >0 với mọi x (điều 2)

    Từ (điều 1) và (điều 2)

    => m ∈ (-2; 14)

     Trả lời hay
    2 Trả lời 16/08/22
  • Captain
    Captain

    Bất phương trình bậc hai

    Bất phương trình bậc hai ẩn x là bất phương trình dạng ax2 + bx + c < 0 (hoặc ax2 + bx + c ≤ 0 , ax2 + bx + c > 0, ax2 + bx + c ≥ 0), trong đó a, b, c là những số thực đã cho, a ≠ 0.
    0 Trả lời 16/08/22
  • Bơ
    Bơ

    Giải bất phương trình bậc hai

    Giải bất phương trình bậc hai ax2 + bx + c < 0 thực chất là tìm các khoảng mà trong đó f(x) = ax2 + bx + c cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a > 0).

    Người ta đã chứng minh được định lí về dấu tam thức bậc hai sau đây

    Định lý

    Cho f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac.

    Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R.

    Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi x = -b/2a

    Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x1 hoặc x > x2, trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 (x1 < x2) là hai nghiệm của f(x).
    0 Trả lời 16/08/22
Tìm thêm: Toán 10 bài tập Toán 10
Câu hỏi mới
Danh mục
Hỏi bài ngay thôi!
×

Gửi câu hỏi/bài tập

Thêm vào câu hỏi
Đăng

Hỏi đáp Toán 10
Xem thêm