Giaitoan.com Toán 11

Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác Hàm số lượng giác

Nội dung
  • 2 Đánh giá

Cách tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác

GiaiToan.com xin giới thiệu tới quý thầy cô và học sinh tài liệu Hàm số lượng giác lớp 11. Nội dung tài liệu gồm lý thuyết, ví dụ minh họa và câu hỏi trắc nghiệm cùng đáp án về hàm số lượng giác hỗ trợ quá trình ôn luyện cho bạn đọc. Tài liệu được GiaiToan biên soạn và đăng tải, hi vọng sẽ giúp các bạn ôn tập kiến thức môn Toán 11 hiệu quả, sẵn sàng cho những kì thi sắp tới. Mời các bạn tham khảo và tải về miễn phí tại đây!

A. Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác

a. Hàm số lượng giác có dạng bậc nhất y = at + b

Thường các hàm số t là các hàm số sin hoặc cos có miền giá trị là một đoạn.

+ Kiến thức cần nhớ −1 ≤ sinx ≤ 1, −1 ≤ cosx ≤ 1

b. Hàm số lượng giác có chứa căn bậc hai

- Hàm số căn bậc 2 của x là hàm số đồng biến và có tập xác định là các số không âm.

c. Hàm số lượng giác có dạng y = at² + bt + c (a ≠ 0)

Giải bài toán bằng cách đặt ẩn phụ. Sau đó tiến hành tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn, khoảng.

d. Hàm số lượng giác có dạng hàm số bậc nhất đối với sinx và cosx

sử dụng điều kiện có nghiệm. Điều kiện có nghiệm của phương trình bậc nhất đối với sin x và cos x là:

Phương trình a.sinx + b.cosx = c có nghiệm khi và chỉ khi {c^2} \leqslant {a^2} + {b^2}

C. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác

Ví dụ 1: Tìm giá trị lớn nhất, nhỏ nhất của hàm số: y = 4sin x.cos x + 1

Hướng dẫn giải

Ta có: y = 4sin x.cos x + 1 = 2 sin 2x + 1

Do -1 ≤ sin2x ≤ 1

=> -2 ≤ sin 2x ≤ 2

=> -2 + 1 ≤ sin 2x + 1 ≤ 2 + 1

=> - 1 ≤ sin 2x + 1 ≤ 3 hay -1 ≤ y ≤ 3

y = 3 khi và chỉ khi \sin 2x = 1 \Rightarrow x = \frac{\pi }{4} + k\pi (k \in \mathbb{Z})

y = -1 khi và chỉ khi \sin 2x = - 1 \Rightarrow x = - \frac{\pi }{4} + k\pi (k \in \mathbb{Z})

Vậy giá trị lớn nhất của hàm số là 2, giá trị nhỏ nhất của hàm số là -1

Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y = 4 – 3 sin2x

Hướng dẫn giải

Ta có: 0 ≤ sin2x ≤ 1

=> -3 ≤ -3sin2x ≤ 0

=> 4 - 3 ≤ y ≤ 0

y = 4 khi và chỉ khi {\sin ^2}x = 1 \Rightarrow {\cos ^2}x = 0 \Rightarrow \cos x = 0 \Rightarrow x = \frac{\pi }{2} + k\pi (k \in \mathbb{Z})

y = 1 khi và chỉ khi {\sin ^2}x = 0 \Rightarrow \sin x = 0 \Rightarrow x = k\pi (k \in \mathbb{Z})

Vậy giá trị lớn nhất của biểu thức là 4, giá trị nhỏ nhất của biểu thức là 1

Ví dụ 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y = 6cos2x + 2cos22x

Hướng dẫn giải

Ta có:

\begin{matrix} y = 6{\cos ^2}x + {\cos ^2}2x \hfill \\ = 6{\cos ^2}x + {(2{\cos ^2}x - 1)^2} \hfill \\ = 4{\cos ^4}x + 2{\cos ^2}x + 1 \hfill \\ \end{matrix}

Đặt t = {\cos ^2}x,t \in \left[ {0,1} \right] ta có hàm số y = 4t2 + 2t + 1

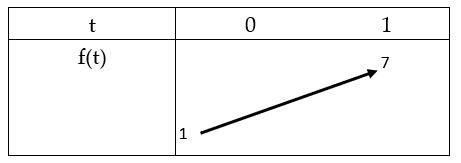
Tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác

Giá trị lớn nhất của hàm số là 7 khi \cos x = 1 \Rightarrow x = k2\pi (k \in \mathbb{Z})

Giá trị nhỏ nhất của hàm số là 1 khi \cos x = 0 \Rightarrow x = \frac{\pi }{2} + k2\pi (k \in \mathbb{Z})

Ví dụ 4: Tìm giá trị lớn nhất, nhỏ nhất của hàm số:

a. y = 3\sin x + 4\cos x + 5

b. y = \sqrt {2\sin x + 3}

Hướng dẫn giải

a. Xét phương trình:

\begin{matrix} y = 3\sin x + 4\cos x + 5 \hfill \\ \Leftrightarrow 3\sin x + 4\cos x + 5 - y = 0 \hfill \\ \end{matrix}

Để phương trình có nghiệm

\begin{matrix} \Leftrightarrow {3^2} + {4^2} \geqslant {(5 - y)^2} \hfill \\ \Leftrightarrow {y^2} - 10y \leqslant 0 \hfill \\ \Leftrightarrow 0 \leqslant y \leqslant 10 \hfill \\ \end{matrix}

Vậy hàm số có giá trị lớn nhất là 10, giá trị nhỏ nhất là 0

b. Ta có:

\begin{matrix} - 1 \leqslant \sin x \leqslant 1 \hfill \\ \Rightarrow - 2 \leqslant 2\sin x \leqslant 2 \hfill \\ \Rightarrow - 2 + 3 \leqslant 2\sin x + 3 \leqslant 2 + 3 \hfill \\ \Rightarrow 1 \leqslant 2\sin x + 3 \leqslant 5 \hfill \\ \Rightarrow 1 \leqslant y \leqslant 5 \hfill \\ \end{matrix}

y = 5 khi và chỉ khi \Rightarrow x = \frac{\pi }{2} + k2\pi (k \in \mathbb{Z})

y = 1 khi và chỉ khi \sin x = 0 \Rightarrow x = k2\pi (k \in \mathbb{Z})

Vây giá trị lớn nhất của hàm số là 5

Giá trị nhỏ nhất của hàm số là 1

------------------------------------------------

Trên đây GiaiToan đã chia sẻ đến các bạn học sinh Cách tìm giá trị lớn nhất nhỏ nhất của hàm số lượng giác nhằm cung cấp cơ sở kiến thức ôn tập cho các bạn học sinh, giúp các bạn tiếp xúc với nhiều dạng bài về hàm số lượng giác. Chúc các bạn ôn tập thật tốt!

  • 159 lượt xem
Chia sẻ bởi: Đường tăng
Tìm thêm: Toán 11
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Chuyên đề Toán 11