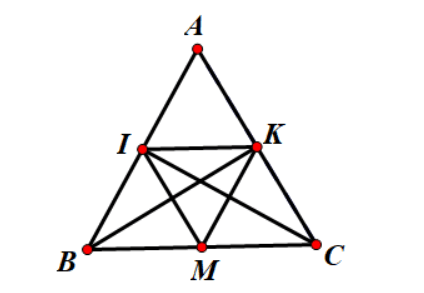
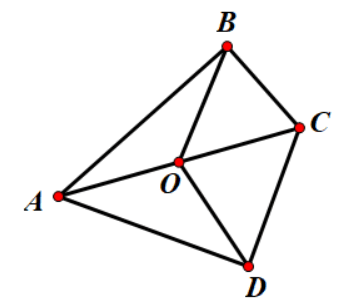
-
 Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 câu trả lờiThích Bình luận -
 Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 câu trả lờiThích Bình luận -
 Nguyễn Huy Hỏi bài Thích Bình luận
Nguyễn Huy Hỏi bài Thích Bình luận -
 Lê Thị Thùy Hỏi đáp Toán 8Hỏi bài 2 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 8Hỏi bài 2 1 câu trả lờiThích Bình luận -
 Hiếu Phan Hỏi bài Thích Bình luận
Hiếu Phan Hỏi bài Thích Bình luận -
 Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận -
 Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận -
 Nguyen Tuan Hỏi bài 1 4 câu trả lờiThích Bình luận Xem thêm 3 câu trả lời
Nguyen Tuan Hỏi bài 1 4 câu trả lờiThích Bình luận Xem thêm 3 câu trả lời -
 Lê Thị Thùy Hỏi đáp Toán 4Hỏi bài 4 3 câu trả lờiThích Bình luận Xem thêm 2 câu trả lời
Lê Thị Thùy Hỏi đáp Toán 4Hỏi bài 4 3 câu trả lờiThích Bình luận Xem thêm 2 câu trả lời -
 Lê Thị Thùy Hỏi đáp Toán 6Hỏi bài 5 5 câu trả lờiThích Bình luận Xem thêm 4 câu trả lời
Lê Thị Thùy Hỏi đáp Toán 6Hỏi bài 5 5 câu trả lờiThích Bình luận Xem thêm 4 câu trả lời -
 Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 9Hỏi bài 1 1 câu trả lờiThích Bình luận -
 Lê Thị Thùy Hỏi đáp Toán 6Hỏi bài 8 1 câu trả lờiThích Bình luận
Lê Thị Thùy Hỏi đáp Toán 6Hỏi bài 8 1 câu trả lờiThích Bình luận
Gợi ý cho bạn
-
Luyện tập 4 trang 37 Toán 6 tập 2 SGK Cánh Diều
Giải Toán 6 Tập 2 -
Bài toán trang 43 Toán 6 tập 2 SGK Kết nối tri thức với cuộc sống
Giải Toán 6 Kết nối tri thức -

Bài tập cuối tuần Toán lớp 4 Cánh diều - Tuần 19
Bài tập cuối tuần Toán lớp 4 -
Luyện tập 5 trang 37 Toán 6 tập 2 SGK Cánh Diều
Giải Toán 6 Tập 2 -
Tìm số hữu tỉ a, biết rằng lấy a nhân với 1/2 rồi cộng với 3/4
Giải Toán 7 Chân trời sáng tạo -
Bài 5 trang 8 Toán lớp 2 tập 2 SGK Cánh Diều
Giải Toán lớp 2 -
Bài tập cuối tuần lớp 5 môn Toán - Tuần 18
Phiếu bài tập cuối tuần lớp 5 -
Câu hỏi trang 44 Toán 6 tập 2 SGK Kết nối tri thức với cuộc sống
Giải Toán 6 Kết nối tri thức -
Luyện tập trang 62 Toán 7 tập 1 SGK Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức -
Thử thách nhỏ trang 8 Toán 6 tập 2 SGK Kết nối tri thức với cuộc sống
Giải Toán 6 Kết nối tri thức