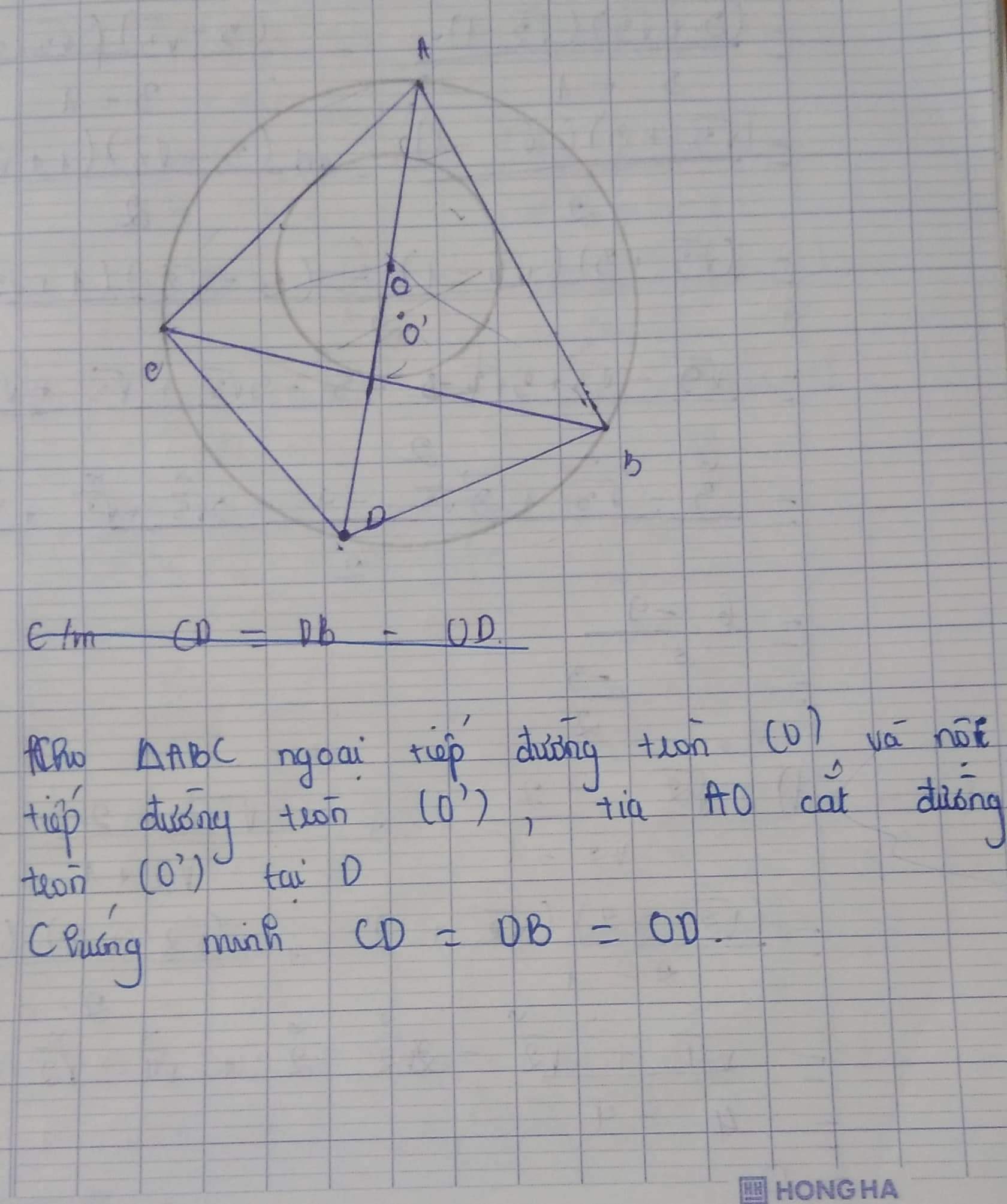
CM CD=DB=OD

Một đội xe theo kế hoạch chở hết 200 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó
chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 25 tấn. Tính thời gian đội chở hết hàng theo kế hoạch.

Cho tam giác ABC có ba góc nhọn, đường cao AD. Đường tròn (O) đường kính BC cắt AC tại E, AD cắt BE tại H.

1) Chứng minh CDHE là tứ giác nội tiếp.

2) Gọi giao điểm của CH với AB là F. Chứng minh F thuộc đường tròn (O) và DA là phân giác
của góc EDF.

3) Kẻ các tiếp tuyến AM, AN với (O) (M, N là tiếp điểm), AO cắt MN tại K, đoạn thẳng AH cắt
(O) tại P. Gọi I là tâm đường tròn ngoại tiếp ∆OPK . Chứng minh B, C, I thẳng hàng.

Tìm m để phương trình x⁴ + (2m - 3)x² - 2m + 2 = 0 có bốn nghiệm phân biệt.

Tháng thứ nhất hai tổ sản xuất được 500 sản phẩm. Sang tháng thứ hai, do cải tiến kĩ thuật, tổ 1 làm vượt mức 10%, tổ 2 làm vượt mức 15% so với tháng thứ nhất. Vì vậy, tháng thứ hai cả hai tổ đã làm được 564 sản phẩm. Hỏi trong tháng thứ nhất mỗi tổ sản xuất được bao nhiêu sản phẩm?

Trục lăn của một cái lăn sơn có dạng một hình trụ. Đường kính của đường tròn đáy là 8cm, chiều dài trục lăn là 30cm. Sau khi lăn được 10 vòng thì trục lăn tạo trên sân phẳng một diện tích là bao nhiêu? (lấy π ≈ 3,14).

Giải phương trình:

Chứng minh rằng ta có bất đẳng thức

Cho a, b, c, d là các số thực dương thỏa mãn điều kiện

Cho biểu thức  và ( với )

a) Tính giá trị của biểu thức A khi x = 36

b) Chứng minh rằng B = 2

c) Đặt M = A - B. Tìm các giá trị nguyên của x để

Bài 1:

a) Tìm điều kiện của x để biểu thức   xác định

b) Rút gọn biểu thức:

c) Giải phương trình:

d) Chứng minh rằng:

Bài 1: Thực hiện phép tính

a)

b)

c)

Bài 3: Giải các phương trình sau:

a)

b)