Hệ thức về cạnh và đường cao Chuyên đề Toán lớp 9 luyện thi vào lớp 10

1 Đánh giá

Hệ thức lượng trong tam giác vuông

A. Công thức hệ thức về cạnh và đường cao trong tam giác vuông
B. Bài tập hệ thức về cạnh và đường cao trong tam giác vuông

Chuyên đề Toán 9: Hệ thức lượng trong tam giác là một dạng toán khó thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

Hệ thức về cạnh và đường cao trong tam giác vuông

A. Công thức hệ thức về cạnh và đường cao trong tam giác vuông

Khi giải các bài toán liên quan đến cạnh và đường cao trong tam giác vuông, ngoài việc nắm vững các kiến thức về định lý Talet, về các trường hợp đồng dạng của tam giác, cần phải nắm vững các kiến thức sau:

Cho tam giác ABC vuông tại A, đường cao AH, ta có:

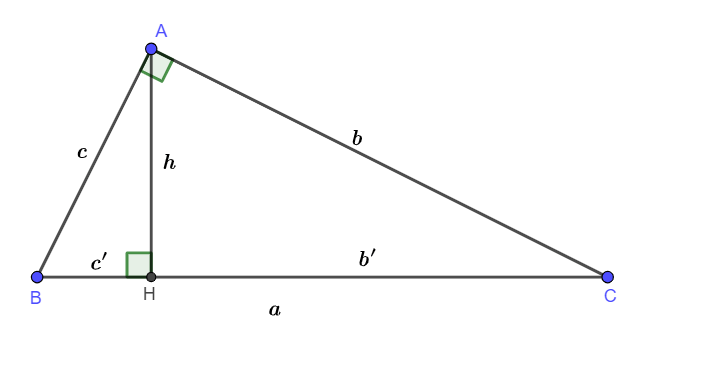
Hệ thức về cạnh và đường cao

${a^2} = {b^2} + {c^2}$	${b^2} = a.b';{c^2} = a.c'$	${h^2} = b'.c'$
$a.h = b.c$	$\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$	$\frac{{b'}}{a} = \frac{{{b^2}}}{{{a^2}}}$

- Diện tích tam giác vuông: $S = \frac{1}{2}ab$

B. Bài tập hệ thức về cạnh và đường cao trong tam giác vuông

Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21

a) Tính các cạnh của tam giác ABC.

b) Tính độ dài các đoạn AH, BH, CH.

Hướng dẫn giải

Hình vẽ minh họa:

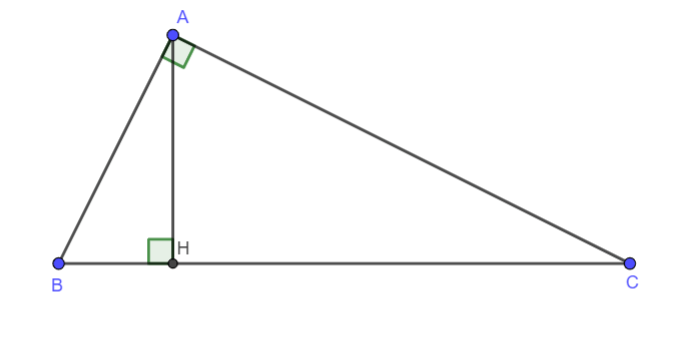
Hệ thức về cạnh và đường cao

a). Theo giả thiết: AB : AC = 3 : 4

=> $\frac{{AB}}{3} = \frac{{AC}}{4} = \frac{{AB + AC}}{{3 + 4}} = 3$

=> AB = 3.3 = 9(cm); AC = 3.4 = 12 (cm)

Tam giác ABC vuông tại A, theo định lý Pi – ta - go ta có:

BC² = AB² + AC² = 9² + 12² = 225

=> BC = 15cm

b) Tam giác ABC vuông tại A, ta có AH.BC = AB . AC

=> $AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2\left( {cm} \right)$

AH² = BH . HC.

Đặt BH = x (0 < x < 9) thì HC = 15 - x, ta có:

$\begin{matrix} {\left( {7,2} \right)^2} = x\left( {15 - x} \right) \hfill \\ \Leftrightarrow {x^2} - 15x + 51,84 = 0 \hfill \\ \Leftrightarrow x\left( {x - 5,4} \right) = 9,6\left( {x - 5,4} \right) = 0 \hfill \\ \Leftrightarrow \left( {x - 5,4} \right)\left( {x - 9,6} \right) = 0 \hfill \\ \end{matrix}$

=> x = 5,4 hoặc (loại)

Vậy BH = 5,4cm

HC = BC – BH = 9,6 cm

Ví dụ 2: Cho ABC tam giác cân có đáy BC = 2a, cạnh bên bằng b (b > a).

a) Tính diện tích tam giác ABC

b) Dựng $BK \bot AC$ . Tính tỷ số $\frac{{AK}}{{AC}}$

Hướng dẫn giải

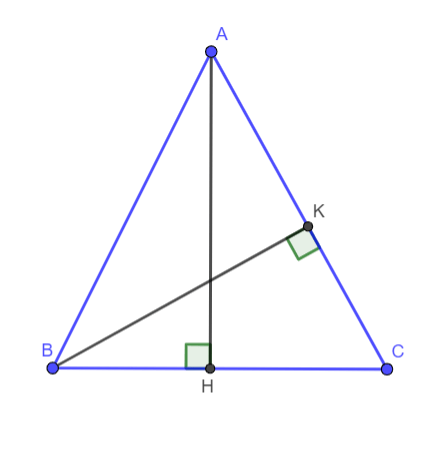
Hệ thức về cạnh và đường cao

a). Gọi H là trung điểm của BC. Theo định lý Pitago ta có:

$A{H^2} = A{C^2} - H{C^2} = {b^2} - {a^2}$

=> ${S_{ABC}} = \frac{1}{2}BC.AH = \frac{1}{2}a\sqrt {{b^2} - {a^2}}$

$\Rightarrow AH = \sqrt {{b^2} - {a^2}}$

b) $\frac{1}{2}BC.AH = \frac{1}{2}BK.AC = {S_{ABC}}$ Ta có:

=> $BK = \frac{{BC.AH}}{{AC}} = \frac{{2a}}{b}\sqrt {{b^2} - {a^2}}$

Áp dụng định lý Pitago trong tam giác vuông AKB ta có:

$A{K^2} = A{B^2} - B{K^2} = {b^2} - \frac{{4{a^2}}}{{{b^2}}}\left( {{b^2} - {a^2}} \right) = \frac{{{{\left( {{b^2} - 2{a^2}} \right)}^2}}}{{{b^2}}}$

=> $AK = \frac{{\left| {{b^2} - 2{a^2}} \right|}}{b}$

=> $\frac{{AK}}{{AC}} = \frac{{\left| {{b^2} - 2{a^2}} \right|}}{{{b^2}}}$

Ví dụ 3: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c.

a) Tính diện tích tam giác ABC theo a

b) Chứng minh: ${a^2} + {b^2} + {c^2} \geqslant 4\sqrt 3 S$

Hướng dẫn giải

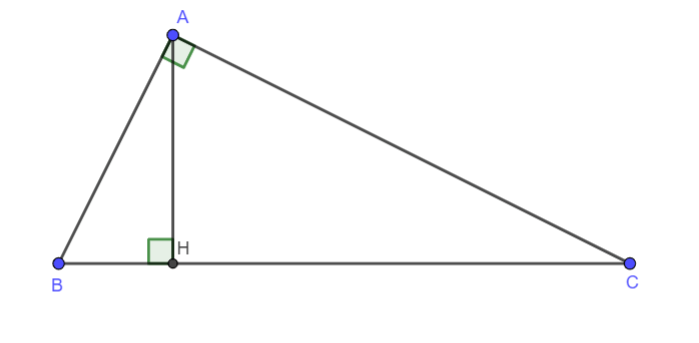
Hệ thức về cạnh và đường cao

a). Ta giả sử góc A là góc lớn nhất của tam giác ABC

=> B, C là các góc nhọn. Suy ra chân

đường cao hạ từ A lên BC là điểm

H thuộc cạnh BC.

Ta có: BC = BH + HC.

Áp dụng định lý Pi ta go cho các tam giác vuông AHB, AHC

Ta có: $A{B^2} = A{H^2} + H{B^2},A{C^2} = A{H^2} + H{C^2}$

Trừ hai đẳng thức trên ta có:

${c^2} - {b^2} = H{B^2} - H{C^2} = \left( {HB + HC} \right)\left( {HB - HC} \right) = a.\left( {HB - HC} \right)$

$\Rightarrow HB - HC = \frac{{{c^2} - {b^2}}}{a}$

Ta cũng có: $HB + HC = a \Rightarrow BH = \frac{{{a^2} + {c^2} - {b^2}}}{{2a}}$

Áp dụng định lý Pitago cho tam giác vuông AHB

$\Rightarrow A{H^2} = {c^2} - {\left( {\frac{{{a^2} + {c^2} - {b^2}}}{{2a}}} \right)^2} = \left( {c - \frac{{{a^2} + {c^2} - {b^2}}}{{2a}}} \right)\left( {c + \frac{{{a^2} + {c^2} - {b^2}}}{{2a}}} \right)$

$= \left[ {\frac{{{{\left( {a + c} \right)}^2} - {b^2}}}{{2a}}} \right].\left[ {\frac{{{b^2} - {{\left( {a - c} \right)}^2}}}{{2a}}} \right] = \frac{{\left( {a + b + c} \right)\left( {a + c - b} \right)\left( {b + a - c} \right)\left( {b + c - a} \right)}}{{4{a^2}}}$

Đặt 2p = a + b + c thì

$A{H^2} = \frac{{16p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{{4{a^2}}} \Rightarrow AH = 2\frac{{\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}{a}$

Từ đó tính được $S = \frac{1}{2}BC.AH = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

b) Từ câu a) ta có: $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Áp dụng bất đẳng thức Cô si ta có:

$\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \leqslant {\left( {\frac{{p - a + p - b + p - c}}{3}} \right)^3} = \frac{{{p^3}}}{{27}}$

=> $S \leqslant \sqrt {p.\frac{{{p^3}}}{{27}}} = \frac{{{p^2}}}{{3\sqrt 3 }}$

Hay $S \leqslant \frac{{{{\left( {a + b + c} \right)}^2}}}{{12\sqrt 3 }}$

Mặt khác ta dễ chứng minh được: ${\left( {a + b + c} \right)^2} \leqslant 3\left( {{a^2} + {b^2} + {c^2}} \right)$

=> $S \leqslant \frac{{3\left( {{a^2} + {b^2} + {c^2}} \right)}}{{12\sqrt 3 }} \Leftrightarrow {a^2} + {b^2} + {c^2} \geqslant 4\sqrt 3 S$

Dấu bằng xảy ra khi và chỉ khi tam giác ABC đều.

------------------------------------------

Hy vọng tài liệu Công thức hệ thức lượng trong tam giác vuông Toán 9 sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi biểu thức chứa căn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Chia sẻ bởi: