Đề thi học kì 1 Toán 7 Đề 1 Đề thi cuối kì 1 Toán 7

40 Đánh giá

Đề thi học kì 1 lớp 7

Đề thi cuối kì 1 Toán 7 - Đề 1
Đáp án Đề thi cuối kì 1 Toán 7 Đề 1

Đề thi học kì 1 môn Toán lớp 7 - Đề 1 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình Toán lớp 7 giúp học sinh ôn tập, củng cố kiến thức đầy đủ, chuẩn bị tốt cho những bài kiểm tra sắp tới. Chúc các em học sinh ôn tập thật tốt!

A. Đề thi cuối kì 1 Toán 7 - Đề 1

PHÒNG GD&ĐT ……..

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng.

Câu 1: Kết quả của phép tính $- \frac{8}{5} + \frac{2}{3}$

A. $\frac{{ - 2}}{5}$	B. $- \frac{{14}}{{15}}$
C. $\frac{1}{{15}}$	D. $\frac{{ - 7}}{3}$

Câu 2: Điểm nào sau đây thuộc đồ thị của hàm số y = 2x + 14

A. $\left( { - 7,0} \right)$	B. $\left( {1, - 1} \right)$
C. $\left( {0,7} \right)$	D. $\left( {1,2} \right)$

Câu 3: Cho tỉ lệ thức $\frac{{ - 3x}}{4} = \frac{{120}}{5}$ . Giá trị của x bằng bao nhiêu?

A. -32	B. -15
C. -24	D. -7

Câu 4: Nếu |4x| - 1 = 7 thì

A. $x = \pm 4$	B. $x = \pm 2$
C. x = -7	D. x = 1

Câu 5: Cho 4 đường thẳng phân biệt đồng quy tại một điểm. Khi đó, có bao nhiêu cặp góc kề bù được tạo thành?

A. 4 cặp	B. 8 cặp
C. 12 cặp	D. 24 cặp

Câu 6: Trong các khẳng định dưới đây, khẳng định nào đúng?

A. Hai góc có chung đỉnh và bằng nhau là hai góc đối đỉnh.

B. Hai góc bằng nhau thì đối đỉnh.

C. Hai góc đối đỉnh thì bằng nhau.

D. Hai góc có một cạnh của góc này là tia đối một cạnh của góc kia là hai góc đối đỉnh.

Câu 7: Cho các đường thẳng a, b, c. Nếu $a \bot b,b//c$ thì

A. $a \bot c$	B. a // c
C. a // b	D. c // b

Câu 8: Cho tam giác ABC và tam giác MNP có BC = PN, $\widehat {ACB} = \widehat {MPN}$ . Cần thêm điều kiện nào sau đây để $\Delta ABC = \Delta MNP$ theo trường hợp góc – cạnh - góc?

A. $MN = AB$	B. $\widehat {ABC} = \widehat {MNP}$
C. $\widehat {BAC} = \widehat {NMP}$	D. $AC = MP$

II. PHẦN TỰ LUẬN (7 điểm)

Câu 1: Thực hiện phép tính:

a) $\left( {\frac{{ - 1}}{4} + \frac{1}{3}} \right):\frac{5}{{11}} + \left( {\frac{{ - 3}}{4} + \frac{2}{3}} \right):\frac{5}{{11}}$

b) $- 3\frac{1}{2} + 1\frac{1}{2} + \left( { - 3} \right).\left( {\frac{3}{4} - 0,25} \right)$

Câu 2: Tìm giá trị của x biết:

a. $\left| {x + 1} \right| - 1\frac{3}{4}:\frac{5}{4} = 2 - \frac{2}{5}$

b. ${3^{x + 2}} - 24 = {3^x}$

Câu 3:

1) Ba lớp 7A, 7B, 7C tham gia kế hoạch thu gom giấy vụn bảo vệ môi trường được tổng cộng 120kg giấy. Biết số giấy mỗi lớp thu được tỉ lệ với 7; 8; 9. Tính số giấy mỗi lớp thu được?

2) Cho hai đại lượng tỉ lệ nghịch x và y, x₁ và x₂ là 2 giá trị của x, y₁ và y₂ là 2 giá trị tương ứng của y. Biết x₁ = 5, x₂ = 2; y₁+ y₂ = 21. Tính y₁, y_2.

Câu 4: Cho ∆ABC, MB = MC. Từ M kẻ ME ⊥ AB (E ∈ AB), MF ⊥ AC (F ∈ AC). Chứng minh rằng:

a) ∆AMB = ∆AMC

b) EA = FA

c) EF // BC

Câu 5: Tính giá trị lớn nhất của biểu thức $T = \left| {a - 2018} \right| - \left| {a - 2017} \right|$

B. Đáp án Đề thi cuối kì 1 Toán 7 Đề 1

1. Đáp án trắc nghiệm

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5	Câu 6	Câu 7	Câu 8
B	A	A	B	D	C	A	B

2. Đáp án tự luận

Câu 1:

a) $\left( {\frac{{ - 1}}{4} + \frac{1}{3}} \right):\frac{5}{{11}} + \left( {\frac{{ - 3}}{4} + \frac{2}{3}} \right):\frac{5}{{11}}$

$= \left( {\frac{{ - 1}}{4} + \frac{1}{3} + \frac{{ - 3}}{4} + \frac{2}{3}} \right):\frac{5}{{11}} = \left( { - 1 + 1} \right):\frac{5}{{11}} = 0$

b) $- 3\frac{1}{2} + 1\frac{1}{2} + \left( { - 3} \right).\left( {\frac{3}{4} - 0,25} \right) = 9.\left( {\frac{3}{4} - \frac{1}{4}} \right) - 2 = 9.\frac{1}{2} - 2 = \frac{5}{2}$

Câu 2:

a) x = 2 hoặc x = -4

b) x = 1

Câu 3:

1) Gọi số giấy thu được của lớp 7A, 7B, 7C lần lượt là: x, y, z, (x, y, z > 0)

Tổng số giấy 3 lớp thu được là 120kg

=> x + y + z = 120(kg)

Ta có: Số giấy mỗi lớp thu được tỉ lệ với 7; 8; 9

=> $\frac{x}{7} = \frac{y}{8} = \frac{z}{9}$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\begin{matrix} \dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{9} = \dfrac{{x + y + z}}{{7 + 8 + 9}} = \dfrac{{120}}{{24}} = 5 \hfill \\ \Rightarrow \dfrac{x}{7} = 5 \Rightarrow x = 7.5 = 35\left( {kg} \right) \hfill \\ \Rightarrow \dfrac{y}{8} = 5 \Rightarrow y = 8.5 = 40\left( {kg} \right) \hfill \\ \Rightarrow \dfrac{z}{9} = 5 \Rightarrow z = 9.5 = 45\left( {kg} \right) \hfill \\ \end{matrix}$

Kết luận: Lớp 7A thu được 35 kg giấy

Lớp 7B thu được 40 kg giấy

Lớp 7C thu được 45 kg giấy

2) Do x, y là hai đại lượng tỉ lệ nghịch $\Rightarrow \frac{{{x_1}}}{{{x_2}}} = \frac{{{y_2}}}{{{y_1}}}\left( * \right)$

Thay x₁ = 5, x₂ = 2 vào (*) ta được:

$\begin{matrix} \dfrac{5}{2} = \dfrac{{{y_1}}}{{{y_2}}} \Rightarrow \dfrac{{{y_2}}}{2} = \dfrac{{{y_1}}}{5} = \dfrac{{{y_2} + {y_1}}}{{2 + 5}} = \dfrac{{21}}{7} = 3 \hfill \\ \Rightarrow \dfrac{{{y_2}}}{2} = \dfrac{{{y_1}}}{5} = 3 \hfill \\ \Rightarrow \dfrac{{{y_2}}}{2} = 3 \Rightarrow {y_2} = 2.3 = 6 \hfill \\ \dfrac{{{y_1}}}{5} = 3 \Rightarrow {y_1} = 3.5 = 15 \hfill \\ \end{matrix}$

Vậy y₁ = 6, y₂ = 15

Câu 4:

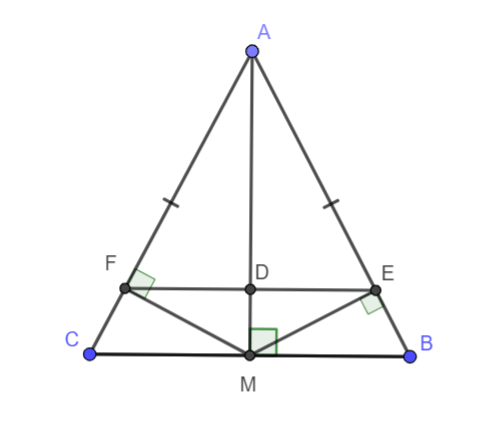
a) Xét ∆AMB và ∆AMC có:

AB = AC (Tam giác ABC cân tại A)

MB = MC (M là trung điểm cạnh BC)

MA là cạnh chung

=> ∆AMB = ∆AMC (c – c – c)

b) Ta có: ∆AMB = ∆AMC (chứng minh câu a)

$\Rightarrow \widehat {BAM} = \widehat {CAM}$ (hai góc tương ứng)

Xét ∆AME và ∆AMF có:

MA là cạnh chung

$\widehat {BAM} = \widehat {CAM}$

=> ∆AME = ∆AMF (cạnh huyền – góc nhọn)

=> EA = FA (hai cạnh tương ứng)

c) Theo chứng minh câu a ta có:

∆AMB = ∆AMC

$\Rightarrow \widehat {AMB} = \widehat {AMC}$

Do hai góc ở vị trí kề bù

$\begin{matrix} \Rightarrow \widehat {AMB} + \widehat {AMC} = {180^0} \hfill \\ \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^0} \hfill \\ \Rightarrow AM \bot BC\left( * \right) \hfill \\ \end{matrix}$

Gọi D là giao điểm của AM và FE.

Xét ∆ADE và ∆ADF có:

$\widehat {DAE} = \widehat {DAF}$ (hai góc tương ứng của ∆AMB và ∆AMC)

AE = AF (chứng minh câu b)

=> ∆ADE = ∆ADF (c – g – c)

$\Rightarrow \widehat {ADE} = \widehat {ADF}$

Mà hai góc ở vị trí kề bù

$\begin{matrix} \Rightarrow \widehat {ADE} + \widehat {ADF} = {180^0} \hfill \\ \Rightarrow \widehat {ADE} = \widehat {ADF} = {90^0} \hfill \\ \Rightarrow EF \bot AM\left( {**} \right) \hfill \\ \end{matrix}$

Từ (*) và (**) => EF // BC

Câu 5:

$T = \left| {a - 2018} \right| - \left| {a - 2017} \right|$

Áp dụng bất đẳng thức $\left| {x - y} \right| \geqslant \left| x \right| - \left| y \right|$

$T = \left| {a - 2018} \right| - \left| {a - 2017} \right| \leqslant \left| {a - 2018 - a + 2017} \right| = 1$

Vậy giá trị lớn nhất của T là 1.

Mời các bạn tải tài liệu miễn phí tham khảo hướng dẫn giải chi tiết!

---------------------------------

Tài liệu liên quan:

Năm học 2021 - 2022

Năm học 2020 - 2021

-------------------------------------------------

Trên đây là Đề thi Toán lớp 7 học kì 1 Đề 1 giaitoan.com giới thiệu tới quý thầy cô và bạn đọc. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Toán lớp 7, Tiếng anh lớp 7, Vật lí lớp 7, Ngữ văn lớp 7,...

Chia sẻ bởi: