Cho hình thang ABCD vuông tại A và D Chuyên đề Toán lớp 9 luyện thi vào lớp 10

2 Đánh giá

Chuyên đề Toán 9: Hình thang vuông

Chuyên đề Toán 9 Cho hình thang vuông ABCD là một dạng toán khó thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

A. Lí thuyết cần nhớ

- Tổng ba góc của một tam giác bằng ${180^0}$

- Lưu ý tính chất các trường hợp đồng dạng của tam giác.

- Định lí Pi – ta – go: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

- Diện tích hình thang bằng tổng hai đáy nhân với chiều cao chia 2.

B. Bài tập ví dụ minh họa

Bài tập 1: Cho hình thang ABCD vuông tại A và D có hai đường chéo vuông góc với nhau tại I.

a. Chứng minh rằng: $\Delta AIB \sim \Delta DAB$

b. Chứng minh rằng: $\Delta AIB \sim \Delta IDC$

c. Cho AB = 4cm, CD = 9cm. Tính độ dài các cạnh DA, IA, IC.

d. Tính tỉ số diện tích: $\frac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}}$

Hướng dẫn giải

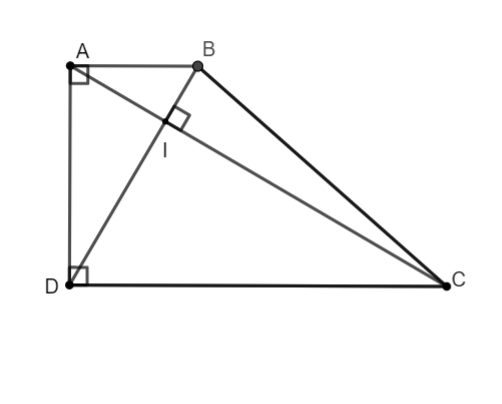
Cho hình thang ABCD vuông tại A và D

a. Xét hai tam giác $\Delta AIB$ và $\Delta DAB$ ta có:

$\widehat {DAB} = \widehat {AIB} = {90^0}$

$\widehat {ABI}$ chung

$\Rightarrow \Delta AIB \sim \Delta DAB$

b. Xét hai tam giác $\Delta AIB$ và $\Delta IDC$ ta có:

$\widehat {DIC} = \widehat {AIB} = {90^0}$ (đối đỉnh)

Do ABCD là hình thang ⇒ AB //CD ⇒ $\widehat {BAI} = \widehat {ICD}$ (So le trong)

$\Rightarrow \Delta AIB \sim \Delta IDC$

c. Ta có: $\Delta AIB \sim \Delta IDC \Rightarrow \frac{{IA}}{{IC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}} = \frac{4}{9}$

$\Rightarrow \frac{{ID}}{{BD}} = \frac{9}{{13}}$

Ta có: Tam giác ABD vuông tại A, AI vuông góc với BD $\Rightarrow A{D^2} = IA.BD = \frac{9}{{13}}D{B^2}$

$\begin{matrix} A{B^2} + A{D^2} = B{D^2} \Rightarrow A{B^2} + A{D^2} = \dfrac{{13}}{9}A{D^2} \hfill \\ \Rightarrow A{B^2} = \dfrac{4}{9}A{D^2} \Rightarrow AB = \dfrac{2}{3}AD \Rightarrow AD = \dfrac{3}{2}AB = 6\left( {cm} \right) \hfill \\ \Rightarrow AC = \sqrt {A{D^2} + D{C^2}} = 3\sqrt {13} \left( {cm} \right) \hfill \\ \end{matrix}$

Ta lại có: $\frac{{IA}}{{IC}} = \frac{4}{9} \Rightarrow IA = \frac{{12\sqrt {13} }}{{13}}\left( {cm} \right)$

c. $\dfrac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}} = \dfrac{{\frac{1}{2}.IC.ID}}{{\dfrac{1}{2}.IA.IB}} = \dfrac{{16}}{{81}}$

Bài tập 2: Cho hình thang vuông ABCD có $\widehat A = \widehat D = {90^0}$ . I là trung điểm của AD, $\widehat {BIC} = {90^0}$ . Chứng minh

a. $\Delta AIB{\text{ }} \sim \Delta DCI$

b. $A{D^2} = 4AB.CD$

Hướng dẫn giải

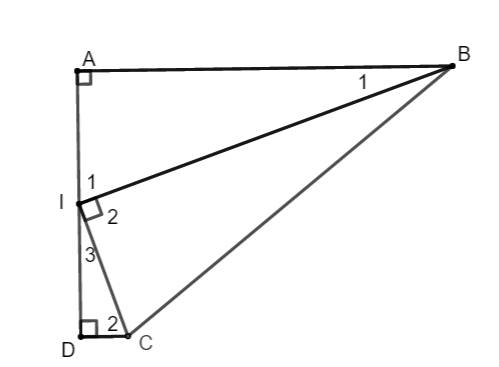
Cho hình thang ABCD vuông tại A và D

a. Xét hai tam giác $\Delta AIB{\text{ }}$ và $\Delta DCI$ ta có:

$\widehat A = \widehat D = {90^0}$

Ta có: $\left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} + \widehat {{B_1}} = {{90}^0}} \\ {\widehat {{I_3}} + \widehat {{C_2}} = {{90}^0}} \end{array}} \right.$ Mà $\widehat {{I_1}} + \widehat {{I_3}} = {90^0} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} = \widehat {{C_2}}} \\ {\widehat {{I_3}} = \widehat {{B_1}}} \end{array}} \right.$

$\Rightarrow \Delta AIB{\text{ }} \sim \Delta DCI$

b. Ta có:

$\begin{matrix} \Delta AIB{\text{ }} \sim \Delta DCI \Rightarrow \dfrac{{AB}}{{DI}} = \dfrac{{AI}}{{CD}} \Rightarrow AB.CD = AI.DI \Rightarrow AB.CD = \dfrac{1}{2}AD.\dfrac{1}{2}AD = \dfrac{1}{4}A{D^2} \hfill \\ \Rightarrow A{D^2} = 4.AB.DC \hfill \\ \end{matrix}$

C. Bài tập tự rèn luyện

Bài 1. Cho hình thang ABCD vuông tại A, đáy nhỏ AB, đường chéo BD vuông góc với BC. Chứng minh rằng:

a. $\widehat {ADB} = \widehat {BCD}$

b. ∆ADB ~ ∆BCD

c. $B{D^2} = AB.DC$
Bài 2. Cho hình thang ABCD có đường chéo BD vuông góc với BC, biết $B{D^2} = AB.DC$
Chứng minh rằng: Tứ giác ABCD là hình thang vuông.

Bài 3: Cho hình thang ABCD vuông tại A và D. Biết CD = 2AB = 2AD và $BC = a\sqrt 2$
a. Tính diện tích hình thang ABCD theo a

b. Gọi I là trung điểm BC, H là chân đường vuông góc từ D xuống AC. Chứng minh rằng:

Bài 4: Cho hình thang ABCD vuông góc tại A và D. Biết AB = AD = 3cm, BC = 6cm. Tính số đo của góc C.

Bài 5: Cho hình thang ABCD vuông tại A và D, có đường chéo DB vuông góc với cạnh bên BC tại B, biết AD= 3cm, AB= 4cm

a) Chứng minh: $\Delta ABD \sim \Delta BDC$

b) Tính độ dài cạnh DC

c) Gọi E là giao điểm của AC và BD. Tính diện tích tam giác AED.

Bài 6: Cho hình thang ABCD (BC là đáy nhỏ). Gọi I là trung điểm của CD. Qua I kẻ đường thẳng d // AB. Kẻ AH và BE vuông góc với d. Chứng minh tứ giác ABCD và tứ giác ABEH có diện tích bằng nhau.

-----------------------------------------------------

Tài liệu liên quan:

------------------------------------------

Hy vọng tài liệu Diện tích hình thang vuông sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi biểu thức chứa căn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Chia sẻ bởi: