Luyện tập 2 trang 24 Toán 10 tập 1 SGK Cánh Diều Giải Toán 10

1 Đánh giá

Luyện tập 2 SGK Toán 10 trang 24

Toán 10 trang 24 Luyện tập 2 là lời giải bài Bất phương trình bậc nhất hai ẩn SGK Toán 10 Cánh Diều được GiaiToan.com biên soạn. Lời giải Toán 10 này với hướng dẫn chi tiết lời giải giúp cho các bạn học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán. Mời các bạn học sinh cùng tham khảo chi tiết.

Giải Luyện tập 2 Toán 10 trang 24

Đề bài: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $x - 2y < 4$

b) $x + 3y \leqslant 6$

Hướng dẫn:

Các bước biểu diễn miền nghiệm của bất phương trình $ax + by < c$ trong mặt phẳng tọa độ $Oxy$ :

+ Bước 1: Vẽ đường thẳng $d:ax + by = c$ . Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng.

+ Bước 2: Lấy một điểm $M\left( {{x_0};{y_0}} \right)$ không nằm trên d (ta thường lấy gốc tọa độ O nếu $c \ne 0$ ). Tính $a{x_0} + b{y_0}$ và so sánh với c.

+ Bước 3: Kết luận:

• Nếu $a{x_0} + b{y_0} < c$ thì nửa mặt phẳng (không kể d) chứa điểm M là miền nghiệm của bất phương trình $ax + by < c$ .

• Nếu $a{x_0} + b{y_0} > c$ thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình $ax + by < c$ .

Lời giải:

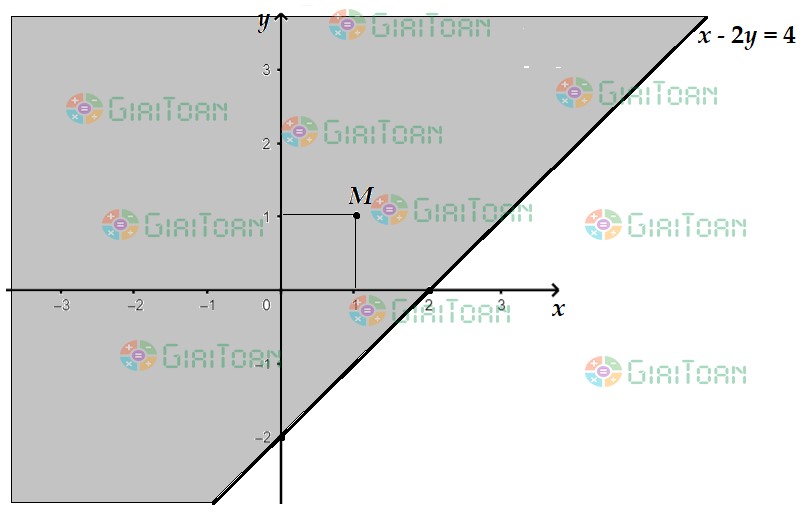
a) $x - 2y < 4$

+ Vẽ đường thẳng $d:x - 2y = 4 \Leftrightarrow y = \frac{1}{2}x - 2$

+ Lấy điểm $M\left( {1;1} \right)$ . Ta có: $1 - 2.1 = - 1 < 4$ .

+ Vậy miền nghiệm của bất phương trình $x - 2y < 4$ là nửa mặt phẳng không bị tô màu, chứa điểm $M\left( {1;1} \right)$ không kể đường thẳng $y = \frac{1}{2}x - 2$ .

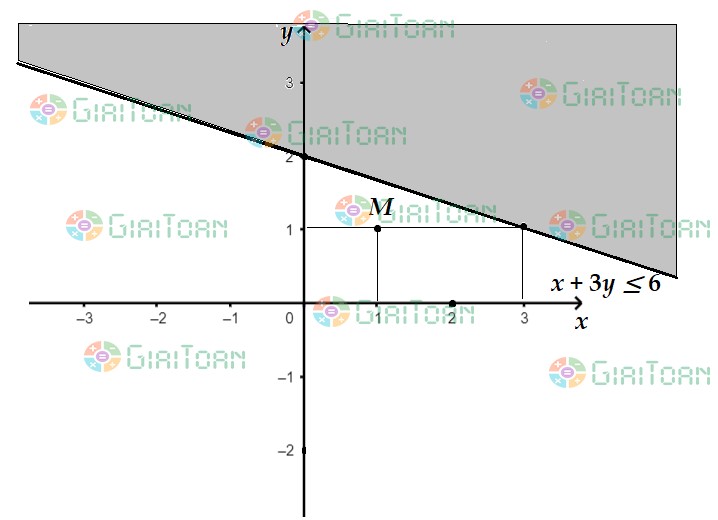
Luyện tập 2 SGK Toán 10 trang 24

b) $x + 3y \leqslant 6$

+ Vẽ đường thẳng $d:x - 2y = 4 \Leftrightarrow y = - \frac{1}{3}x + 2$

+ Lấy điểm $M\left( {1;1} \right)$ . Ta có: $1 + 3.1 = 4 \leqslant 6$ .

+ Vậy miền nghiệm của bất phương trình $x + 3y \leqslant 6$ là nửa mặt phẳng không bị tô màu, chứa điểm $M\left( {1;1} \right)$ kể cả đường thẳng $y = - \frac{1}{3}x + 2$ .

Luyện tập 2 SGK Toán 10 trang 24

-----> Bài tiếp theo: Bài 1 trang 24 Toán 10 tập 1 SGK Cánh Diều

----------------

Trên đây là lời giải chi tiết Toán 10 trang 24 Luyện tập 2 cho các bạn học sinh tham khảo, nắm được cách giải các dạng toán của Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn. Qua đó giúp các bạn học sinh ôn tập chuẩn bị cho các bài thi giữa học kì và cuối học kì lớp 10.

Chia sẻ bởi: