Công thức tính nhanh thể tích khối chóp Thể tích khối chóp

4 Đánh giá

Công thức tính thể tích khối chóp

Công thức tính nhanh thể tích khối chóp tam giác
Công thức tính nhanh thể tích khối chóp tứ giác đều
Thể tích khối bát diện đều

Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, GiaiToan.com xin mời quý thầy cô và các bạn học sinh tham khảo tài liệu Toán 12: Thể tích khối chóp. Bộ tài liệu giới thiệu đến bạn đọc những công thức tính nhanh thể tích khối chóp tam giác đều, tứ giác đều và khối bát diện đều được xây dựng dựa giúp các bạn giải nhanh các câu hỏi trong đề thi THPT Quốc Gia để đạt được kết quả cao nhất

Công thức tính nhanh thể tích khối chóp tam giác

Bài toán	Hình vẽ minh họa	Công thức thể tích
Cho hình chóp S.ABC với các mặt phẳng (SAB), (SBC), (SAC) đôi một vuông góc với nhau, diện tích các tam giác SAB, SBC, SAC lần lượt là S₁, S₂, S₃		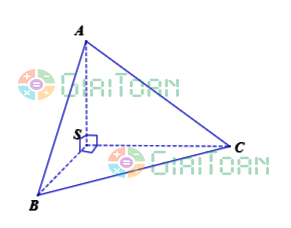${V_{S.ABC}} = \frac{{\sqrt {2{S_1}.{S_2}.{S_3}} }}{3}$
Cho hình chóp S.ABC có SA vuông góc với (ABC), hai mặt phẳng (SAB) và (SBC) vuông góc với nhau, BSC = a, ASB = b		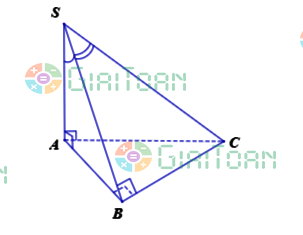${V_{S.ABC}} = \frac{{S{B^3}.\sin 2a.\tan b}}{{12}}$
Cho khối chóp tam giác đều SABC có cạnh đáy bằng a. Gọi (P) là mặt phẳng đi qua A song song với BC và vuông góc với (SBC), góc giữa (P) với mặt phẳng đáy là 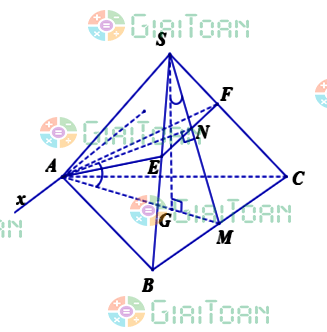$\alpha$		${V_{S.ABC}} = \frac{{{a^3}\cot \alpha }}{{24}}$
Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên bằng b		${V_{S.ABC}} = \frac{{{a^2}\sqrt {3{b^2} - {a^2}} }}{{12}}$
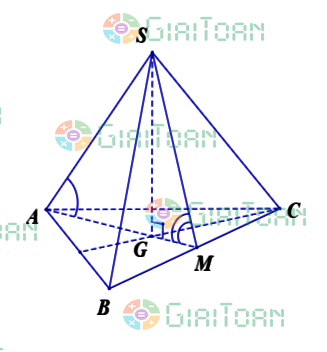
Cho hình chóp tam giác đều S.ABC có đáy bằng a và mặt bên tạo với mặt phẳng đáy một góc $\alpha$		${V_{S.ABC}} = \frac{{{a^3}\tan \alpha }}{{24}}$
Cho hình chóp tam giác đều S.ABC các cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc $\beta$		${V_{S.ABC}} = \frac{{\sqrt 3 {b^3}\sin \beta {{\cos }^2}\beta }}{4}$
Cho hình chóp tam giác đều S.ABC có các cạnh đáy bằng a, cạnh bên tạo với mặt phẳng đáy góc $\beta$		${V_{S.ABC}} = \frac{{{a^3}\tan \beta }}{{12}}$

Công thức tính nhanh thể tích khối chóp tứ giác đều

Bài toán	Hình vẽ minh họa	Công thức thể tích
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, và SA = SB = SC = SD = b		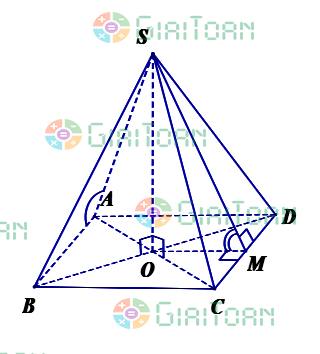${V_{S.ABCD}} = \frac{{{a^2}\sqrt {4{b^2} - 2{a^2}} }}{6}$
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc tạo bởi mặt bên và mặt phẳng đáy là $\alpha$		${V_{S.ABCD}} = \frac{{{a^3}\tan \alpha }}{6}$
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, SAB = $\alpha$ với $\alpha \in \left( {\frac{\pi }{4};\frac{\pi }{2}} \right)$		${V_{S.ABCD}} = \frac{{{a^2}\sqrt {{{\tan }^2}\alpha - 1} }}{6}$
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên bằng a, góc tạo bởi mặt bên và mặt đáy là $\alpha$ với $\alpha \in \left( {0;\frac{\pi }{2}} \right)$		${V_{S.ABCD}} = \frac{{4{a^3}\tan \alpha }}{{3\sqrt {{{\left( {2 + {{\tan }^2}\alpha } \right)}^3}} }}$

Thể tích khối bát diện đều

Bài toán	Hình vẽ minh họa	Công thức thể tích
Khối bát diện đều có đỉnh là tâm các mặt của hình lập phương cạnh a		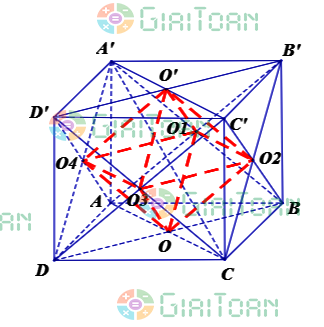$V = \frac{{{a^3}}}{6}$
Cho khối bát diện đều cạnh a. Nối tâm của các mặt bên ta được khối lập phương.		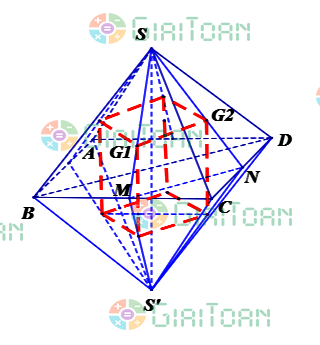$V = {\left( {\frac{{a\sqrt 2 }}{3}} \right)^3} = \frac{{2{a^3}\sqrt 2 }}{{27}}$

----------------------------------------------------

Trên đây GiaiToan đã giới thiệu đến thầy cô và học sinh tài liệu Công thức tính nhanh thể tích hình chóp, hy vọng tài liệu sẽ là công cụ hữu ích giúp học sinh ôn thi THPT Quốc gia hiệu quả.

Một số tài liệu liên quan: