Cho ∆ABC vuông cân tại A, BC = 2cm
. Vẽ ∆ACE vuông cân tại E (E và B khác phía đối với AC). Chứng minh rằng: AECB là hình thang vuông. Tính các góc và cạnh của hình thang vuông AECB.
-
 Đội Trưởng Mỹ Trả lời hay1 Trả lời · 20/07/22
Đội Trưởng Mỹ Trả lời hay1 Trả lời · 20/07/22 -
 Ỉn Trả lời hay1 Trả lời · 20/07/22
Ỉn Trả lời hay1 Trả lời · 20/07/22 -
 Bờm0 Trả lời · 20/07/22
Bờm0 Trả lời · 20/07/22 -
 Nguyễn Thị Huê0 Trả lời · 20/07/22
Nguyễn Thị Huê0 Trả lời · 20/07/22

Hỏi bài
Cách chia đa thức cho đơn thức
Ngày hỏi: 10:58 31/12Sân vườn nhà bạn An hình chữ nhật có chiều rộng 4 m, chiều dài 12 m. Bố Lan thiết kế hai bồn hoa hình thoi kích thước như nhau (như hình vẽ), bên trong bồn hoa trồng hoa hồng, bên ngoài trồng cỏ.
a) Tính chu vi và diện tích sân vườn.
b) Biết mỗi mét vuông cần 4 cây hồng. Tính số cây hồng bố An cần chuẩn bị để trồng đủ vào hai bồn cây.
c) Chi phí trồng cỏ là 55 000 đồng một mét vuông, chi phí mua và trồng một cây hoa hồng là 7 000 đồng. Hỏi bố An cần bao nhiêu tiền để hoàn thiện sân vườn?
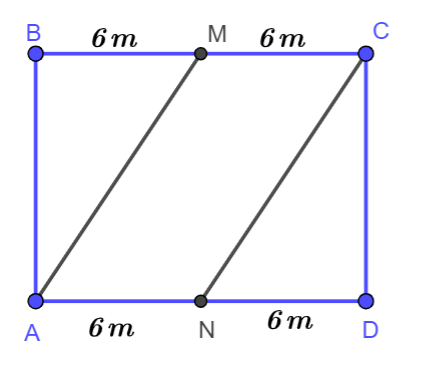
Ngày hỏi: 08:03 29/12 3 câu trả lờiTrên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m, người ta phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở trong khu vực hình bình hành AMCN, cỏ sẽ trồng ở phần đất còn lại. Tiền công để trả cho mỗi mét vuông trồng hoa là 50 000 đồng, trồng cỏ là 40 000 đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
Ngày hỏi: 12:04 27/12 4 câu trả lời