Giaitoan.com Toán 12 Toán 12 Chân trời sáng tạo

Thực hành 1 trang 28 Toán 12 tập 1 Chân trời sáng tạo Giải Toán 12 Chân trời sáng tạo Bài 4

Nội dung
  • 1 Đánh giá

Thực hành 1 trang 28 SGK Toán 12

Toán 12 Thực hành 1 trang 28 tập 1 trong bài Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản SGK Toán 12 Chân trời sáng tạo được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Thực hành 1 Toán 12 trang 28

Thực hành 1 trang 28 toán 12 tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) y = – 2x3 – 3x2 + 1;

b) y = x3 + 3x2 + 3x + 2.

Lời giải chi tiết:

a) Xét hàm số: y = – 2x3 – 3x2 + 1

1. Tập xác định: \mathbb{R}.

2. Sự biến thiên:

  • Chiều biến thiên:

Đạo hàm y' = - 6x2 - 6x;

y' = 0 ⇔ x = 0 hoặc x = - 1.

Trên các khoảng (– ∞; – 1) và (0; + ∞), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

Trên khoảng (– 1; 0), y' > 0 nên hàm số đồng biến trên khoảng đó.

  • Cực trị:

Hàm số đạt cực đại tại x = 0 và yCĐ = 1.

Hàm số đạt cực tiểu tại x = – 1 và yCT = 0.

  • Các giới hạn tại vô cực:

\lim_{x \rightarrow -\infty} y=\lim_{x \rightarrow -\infty}x^3 \left ( -2-\frac{3}{x }+\frac{ 1}{x^3} \right ) =+∞

\lim_{x \rightarrow +\infty} y=\lim_{x \rightarrow +\infty}x^3 \left ( -2-\frac{3}{x }+\frac{ 1}{x^3} \right ) =-∞

  • Bảng biến thiên:

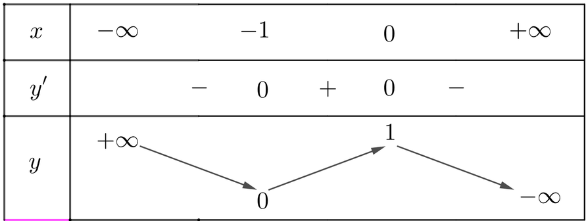
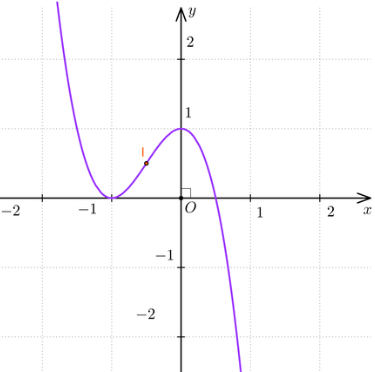
3. Đồ thị

Khi x = 0 thì y = 1 nên (0; 1) là giao điểm của đồ thị với trục Oy.

Ta có y = 0 ⇔ – 2x3 – 3x2 + 1 = 0

⇔ x = - 1 hoặc x=\frac{1}{2}.

Vậy đồ thị của hàm số giao với trục Ox tại hai điểm (- 1; 0) và \left(\frac{1}{2};0\right).

Điểm (0; 1) là điểm cực đại và điểm (- 1; 0) là điểm cực tiểu của đồ thị hàm số.

Đồ thị của hàm số có tâm đối xứng là điểm I\left(-\frac{1}{2};\frac{1}{2}\right).

b) y = x3 + 3x2 + 3x + 2.

Đang cập nhật....

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Chân trời sáng tạo Bài tập cuối chương 1

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 43
Tìm thêm: Toán 12 Toán 12 Chân trời sáng tạo
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần