Giaitoan.com Toán 12 Toán 12 Chân trời sáng tạo

Bài 15 trang 39 Toán 12 tập 1 Chân trời sáng tạo Giải Toán 12 Chân trời sáng tạo Bài tập cuối chương 1

Nội dung
  • 1 Đánh giá

Bài 15 trang 39 SGK Toán 12

Toán 12 Bài 15 trang 39 tập 1 trong bài Bài tập cuối chương 1 SGK Toán 12 Chân trời sáng tạo được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Bài 15 Toán 12 trang 39

Bài 15 trang 39 toán 12 tập 1: Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:

\overline C (x) = 2x - 230 + \frac{{7200}}{x}

a) Khảo sát và vẽ đồ thị hàm số \overline C (x) trên [30; 120].

b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.

Lời giải chi tiết:

a) Xét hàm số y=\overline C (x) = 2x - 230 + \frac{{7200}}{x}

1. Tập xác định: D=[30;120 ]

2. Sự biến thiên:

  • Chiều biến thiên:

Đạo hàm y'=2-\frac{7200}{x^2}; y' = 0 ⇔ x = 60 vì x thuộc [30; 120]

Trên khoảng (30; 60), y' < 0 nên hàm số nghịch biến trên khoảng đó.

Trên khoảng (60; 120), y' > 0 nên hàm số đồng biến trên khoảng đó.

  • Cực trị:

Hàm số đạt cực tiểu tại x = 60 và yCT = 210.

  • Bảng biến thiên:

3. Đồ thị

Điểm cực tiểu của đồ thị hàm số là (60; 210).

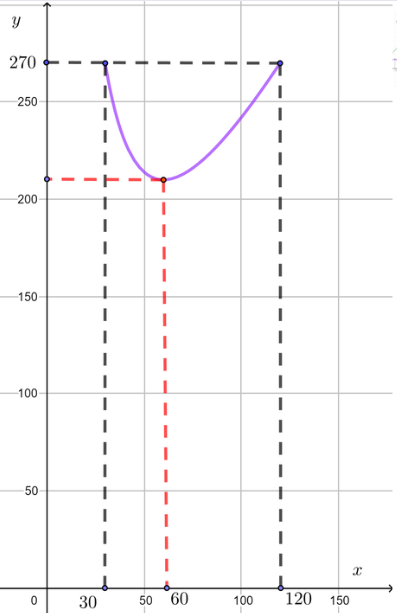
b) Từ đồ thị ta có: \underset{[30;120]}{\min} \overline{C} (x)=\overline{C}(60)=210

Vậy với 60 phần ăn thì chi phí trung bình của một phần ăn là thấp nhất.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Chân trời sáng tạo Bài 1: Vectơ và các phép toán trong không gian

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 78
Tìm thêm: Toán 12 Toán 12 Chân trời sáng tạo
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần