Giaitoan.com Toán 8

Hằng đẳng thức đáng nhớ 7 hằng đẳng thức đáng nhớ Toán 8

Nội dung
  • 3 Đánh giá

Hằng Đẳng Thức

GiaiToan.com xin giới thiệu tới các bạn học sinh tài liệu Những hằng đẳng thức đáng nhớ Toán 8. Bộ tài liệu tổng hợp các công thức khai triển hằng đẳng thức và các bài tập ví dụ minh họa có hướng dẫn chi tiết giúp bạn đọc củng cố và nâng cao kiến thức Toán 8. Chúc các bạn ôn tập hiệu quả!

1. Bình phương của một tổng

{{\left( A+B \right)}^{2}}={{A}^{2}}+2AB+{{B}^{2}}

Phát biểu thành lời: Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích hai số và cộng với bình phương số thứ hai.

Ví dụ minh họa:

a) {x^2} + 2x + 1 = {x^2} + 2.x.1 + {1^2} = {\left( {x + 1} \right)^2}

b) 4{{x}^{2}}+20x+25={{\left( 2x \right)}^{2}}+2.2x.5+{{5}^{2}}={{\left( 2x+5 \right)}^{2}}

c) {{\left( 4x+1 \right)}^{2}}={{\left( 4x \right)}^{2}}+2.4x.1+{{1}^{2}}=16{{x}^{2}}+8x+1

d) {{\left( 3+5x \right)}^{2}}={{3}^{2}}+2.3.5x+{{\left( 5x \right)}^{2}}=9+30x+25{{x}^{2}}

Mở rộng: Bài tập hằng HĐT Bình phương của một tổng

2. Bình phương của một hiệu

{{\left( A-B \right)}^{2}}={{A}^{2}}-2AB+{{B}^{2}}

Phát biểu thành lời: Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích hai số và cộng với bình phương số thứ hai.

Ví dụ minh họa:

a) {{\left( 3-x \right)}^{2}}={{3}^{2}}-3.2.x+{{\left( x \right)}^{2}}=9-6x+{{x}^{2}}

b) {{\left( 5x-2 \right)}^{2}}=({{5x})^{2}}-2.5x.2+{{2}^{2}}=25{{x}^{2}}-20x+4

c) {{x}^{2}}{{y}^{2}}-16x{{y}^{2}}+64{{y}^{2}}={{\left( xy \right)}^{2}}-2.\left( xy \right).8y+{{\left( 8y \right)}^{2}}={{\left( xy-8y \right)}^{2}}

Mở rộng: Bài tập HĐT Bình phương của một hiệu

3. Hiệu hai bình phương

{{A}^{2}}-{{B}^{2}}=\left( A-B \right)\left( A+B \right)

Phát biểu thành lời: Hiệu hai bình phương bằng tích của tổng và hiệu của hai số đó.

Ví dụ minh họa

a) 16-9{{x}^{2}}={{\left( 4 \right)}^{2}}-{{\left( 3x \right)}^{2}}=\left( 4-3x \right)\left( 4+3x \right)

b) \left( 2x+3y \right)\left( 3y-2x \right)=\left( 3y-2x \right)\left( 3y+2x \right)=({{3y})^{2}}-{{\left( 2x \right)}^{2}}={{9y}^{2}}-4{{x}^{2}}

Mở rộng: Bài tập HĐT Hiệu hai bình phương

4. Lập phương của một tổng

{{\left( A+B \right)}^{3}}={{A}^{3}}+3{{A}^{2}}B+3A{{B}^{2}}+{{B}^{3}}

Phát biểu thành lời: Lập phương của một tổng bằng lập phương số thứ nhất cộng ba lần bình phương số thứ nhất nhân với số thứ hai, cộng với ba lần số thứ nhất nhân bình phương số thứ hai rồi cộng với lập phương số thứ hai.

Ví dụ minh họa

a. {{\left( x+2y \right)}^{3}}={{x}^{3}}+3.{{x}^{2}}.2y+3.x.{{\left( 2y \right)}^{2}}+{{\left( 2y \right)}^{3}}={{x}^{3}}+6{{x}^{2}}y+12x{{y}^{2}}+8{{y}^{3}}

b. {{\left( 1+y \right)}^{3}}={{1}^{3}}+{{3.1}^{2}}.y+3.1.{{y}^{2}}+{{y}^{3}}=1+3y+3{{y}^{2}}+{{y}^{3}}

c. {{x}^{3}}+6{{x}^{2}}+12x+8={{x}^{3}}+3.{{x}^{2}}.2+3.x{{.2}^{2}}+{{2}^{3}}={{\left( x+2 \right)}^{3}}

Mở rộng: Bài tập HĐT lập phương của một tổng

5. Lập phương của một hiệu

{{\left( A-B \right)}^{3}}={{A}^{3}}-3{{A}^{2}}B+3A{{B}^{2}}-{{B}^{3}}

Phát biểu thành lời: Lập phương của một tổng bằng lập phương số thứ nhất trừ ba lần bình phương số thứ nhất nhân với số thứ hai, cộng với ba lần số thứ nhất nhân bình phương số thứ hai rồi trừ với lập phương số thứ hai.

Ví dụ minh họa

a. {{\left( x-y \right)}^{3}}={{x}^{3}}-3{{x}^{2}}y+3x{{y}^{2}}+{{y}^{3}}

b. (2-3xy+3{{x}^{2}}{{y}^{2}})-({{y}^{3}}{{x}^{3}}+1)=2-3xy+3{{x}^{2}}{{y}^{2}}-{{x}^{3}}{{y}^{3}}-1=1-3xy+3{{x}^{2}}{{y}^{2}}-{{x}^{3}}{{y}^{3}}

=1-{{3.1}^{2}}.xy+3.1.{{\left( xy \right)}^{2}}-{{\left( xy \right)}^{3}}={{\left( 1-xy \right)}^{3}}

Mở rộng: Bài tập HĐT Bình phương của một hiệu

6. Tổng của hai lập phương

{{A}^{3}}+{{B}^{3}}=\left( A+B \right)\left( {{A}^{2}}-AB+{{B}^{2}} \right)

Phát biểu thành lời: Tổng của hai lập phương bằng tổng hai số đó nhân với bình phương thiếu của hiệu.

Ví dụ minh họa

a) {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)

b) {{\left( 2x-1 \right)}^{3}}=\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)

Mở rộng: Bài tập HĐT Tổng của hai lập phương

7. Hiệu của hai lập phương

{{A}^{3}}-{{B}^{3}}=\left( A-B \right)\left( {{A}^{2}}+AB+{{B}^{2}} \right)

Phát biểu thành lời: Tổng của hai lập phương bằng tổng hai số đó nhân với bình phương thiếu của tổng.

Ví dụ minh họa

8-{{x}^{3}}={{2}^{3}}-{{\left( x \right)}^{3}}=\left( 2-x \right)\left( 4+2x+{{x}^{2}} \right)

Mở rộng: Bài tập HĐT Hiệu của hai lập phương

8. Hằng đẳng thức mở rộng

  • {{\left( A+B+C \right)}^{2}}={{A}^{2}}+{{B}^{2}}+{{C}^{2}}+2AB+2BC+2AC
  • {{\left( A-B+C \right)}^{2}}={{A}^{2}}+{{B}^{2}}+{{C}^{2}}-2AB-2BC+2AC
  • {{\left( A-B-C \right)}^{2}}={{A}^{2}}+{{B}^{2}}+{{C}^{2}}-2AB+2BC+2AC

Hằng đẳng thức

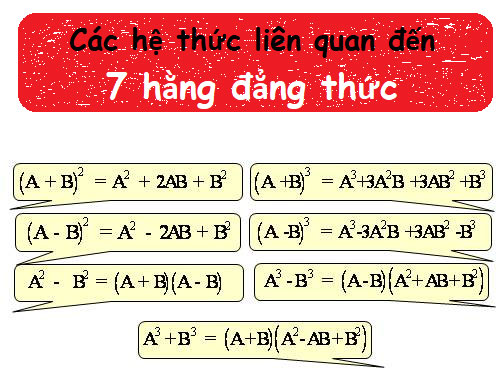
9. Giải bài tập Những hằng đẳng thức đáng nhớ Toán 8:

--------------------------------------------------

Trên đây GiaiToan đã giới thiệu tới bạn đọc tài liệu: Những hằng đẳng thức đáng nhớ. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu, Lý thuyết Toán lớp 8, Giải bài tập Toán 8; Đề thi học kì Toán 8 mà GiaiToan tổng hợp và đăng tải.

Mời bạn đọc tham khảo tài liệu!

  • 476 lượt xem
Chia sẻ bởi: Su kem
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Xem thêm bài viết khác

    Xem thêm Toán 8

    Chủ đề liên quan

    Hằng đẳng thức