Đường thẳng song song với một đường thẳng cho trước Bài tập Toán 8

2 Đánh giá

Đường thẳng song song với một đường thẳng cho trước Toán 8

Bài tập Toán 8: Đường thẳng song song với một đường thẳng cho trước là tài liệu ôn tập với các bài tập chứng minh 2 đường thẳng song song được xây dựng dựa trên trọng tâm chương trình lớp 8, giúp các bạn học sinh luyện tập các dạng Toán lớp 8 đạt kết quả tốt nhất, góp phần củng cố thêm kiến thức.

Hai đường thẳng song song

1. Lí thuyết Đường thẳng song song với một đường thẳng cho trước

Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.

Tính chất: Các điểm cách đường thẳng a một khoảng bằng h nằm trên hai đường thẳng với a và cách a một khoảng bằng h.

Nhận xét: Tập hợp các điểm cách một đường thẳng cố định một khoảng không đổi h không đổi là hai đường thẳng song song vơi đường thẳng đó và cách đường thẳng đó một khoảng bằng h.

Định lí:

+ Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

2. Bài tập đường thẳng song song với một đường thẳng cho trước

Bài tập 1: Cho đường thẳng b. Gọi a và a' là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h, (I) và (II) là các nửa mặt phẳng b. Gọi P, P' là điểm cách đường thẳng b một khoảng bằng h, trong đó có P thuộc nửa mặt phẳng (I), P' thuộc nửa mặt phẳng (II). Chứng minh rằng P thuộc a, P' thuộc a'.

Bài tập 2: Xét tam giác ABC có cạnh BC cố định, đường cao ứng với cạnh BC luôn bằng 2cm. Đỉnh A của các tam giác đó nằm trên đường nào?

Bài tập 3: Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt 2 cạnh AB và AC theo thứ tự tại P và Q; đường thẳng qua Q và song song với AB, cắt BC tại D. Cho biết AP = 6, AQ = 8, BP = 4.

a) Tính độ dài PQ, QC và BC

b) Tính diện tích hình bình hành BPQD

Bài tập 4: Cho tam giác ABC. Vẽ đường thẳng song song với BC cắt AB tại D và cắt AC tại E. Trên tia đối của CA lấy F sao cho CF = BD. Gọi M là giao điểm của DF và BC

a) Chứng minh MD/MF = AC/AB hay MD.AB = MF.AC

b) Cho BC= 8cm, BD = 5cm, DE = 3cm. Chứng minh tam giác ABC cân

3. Lời giải đáp số bài tập chứng minh hai đường thẳng song song

Bài tập 1:

Theo bài ra ta có: Đường thẳng a cách b một khoảng bằng h; điểm P thuộc (I) cũng cách b một khoảng bằng h
=> P thuộc đường thẳng a
Vì chỉ có đường thẳng a mới tập hợp các điểm cách b một quãng bằng h

Bài tập 2:

Điểm A của tam giác ABC đó nằm trên đường thẳng song song với BC và cách BC một quãng bằng 2 cm.

Vì chỉ có đoạn thẳng song song với BC và cách BC một đoạn bằng 2 cm thì tập hợp các điểm cách BC một khoảng bằng 2 cm.

Bài tập 3:

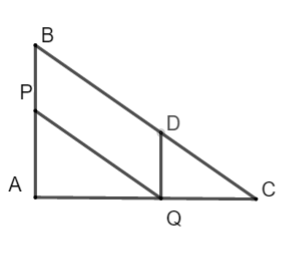
Do PQ // BC nên ta có đẳng thức sau:

$\frac{{AP}}{{AB}} = \frac{{AQ}}{{AC}} = \frac{{PQ}}{{CB}}$

Ta lại có:

$\begin{matrix} PQ = \sqrt {A{Q^2} + A{P^2}} = \sqrt {{6^2} + {8^2}} = 10\left( {cm} \right) \hfill \\ \Rightarrow \dfrac{{AP}}{{AB}} = \dfrac{{PQ}}{{BC}} \hfill \\ \Rightarrow \dfrac{{PQ.AB}}{{AM}} = BC \hfill \\ \Leftrightarrow \dfrac{{10.10}}{6} = BC \Rightarrow BC = \dfrac{{50}}{3}\left( {cm} \right) \hfill \\ AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{\left( {\dfrac{{50}}{3}} \right)}^2} - {{10}^2}} = \dfrac{{40}}{3}\left( {cm} \right) \hfill \\ \Rightarrow QC = AC - AQ = \dfrac{{10}}{3}\left( {cm} \right) \hfill \\ \end{matrix}$

b. ${S_{BPQD}} = \frac{1}{2}.AQ.\left( {BP + QD} \right) = AQ.BP = 8.4 = 32\left( {c{m^2}} \right)$

----------------------------------------------------

GiaiToan.com đã gửi tới các bạn tài liệu Chuyên đề Toán 8: Hai đường thẳng song song. Ngoài ra, các em học sinh có thể tham khảo thêm các tài liệu khác như Giải Toán 8, Giải Bài tập Toán 8, Luyện tập Toán 8, để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao. Chúc các em học tập tốt!

Chia sẻ bởi: