Giaitoan.com Toán 9 Chuyên đề Toán 9 thi vào 10

Tìm điều kiện để hàm số bậc nhất đồng biến nghịch biến Chuyên đề Toán lớp 9 luyện thi vào lớp 10

Nội dung
  • 1 Đánh giá

Chuyên đề Toán 9: Hàm số bậc nhất

GiaiToan.com biên soạn và đăng tải tài liệu Bài tập Toán lớp 9 Xét sự đồng biến, nghịch biến cuar hàm số bậc nhất giúp học sinh hiểu rõ về hàm số bậc nhất, cách vẽ đồ thị hàm số bậc nhất, thế nào là hàm số đồng biến, hàm số nghịch biến, ...Toán lớp 9 nhanh và chính xác nhất. Chi tiết mời các em học sinh cùng tham khảo. Chúc các bạn học tập tốt!

A. Hàm số bậc nhất

- Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a khác 0.

Chú ý: Khi b = 0 hàm số có dạng y = ax (kiến thức lớp 7).

B. Hàm số bậc nhất đồng biến khi nào?

Cho hàm số bậc nhất y = ax + b xác định với mọi giá trị x thuộc \mathbb{R}

=> Hàm số đồng biến trên \mathbb{R} khi a > 0

Hình vẽ minh họa

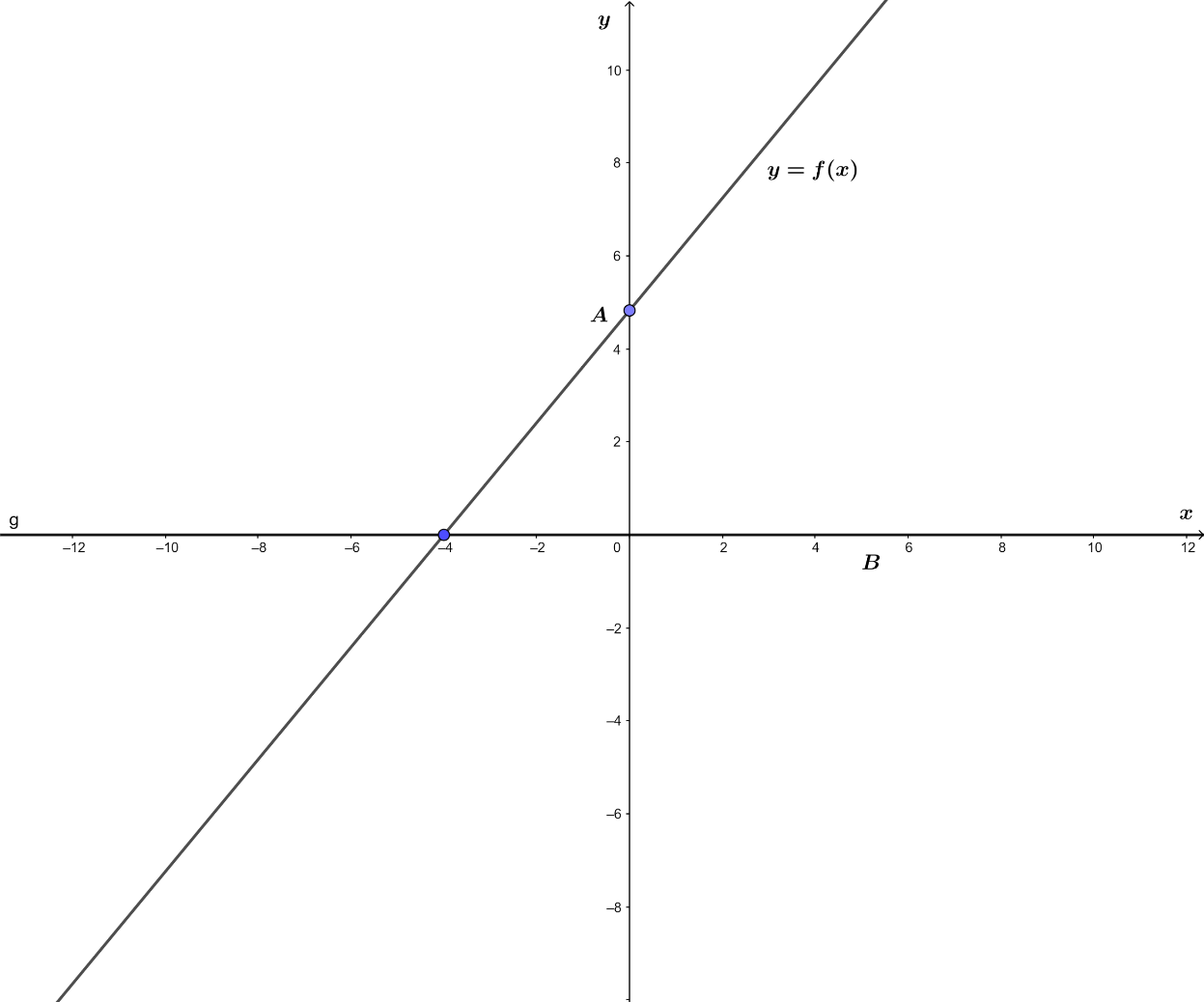
Tìm điều kiện để hàm số bậc nhất đồng biến nghịch biến

C. Hàm số bậc nhất nghịch biến khi nào?

Cho hàm số bậc nhất y = ax + b xác định với mọi giá trị x thuộc \mathbb{R}

=> Hàm số đồng biến trên \mathbb{R} khi a < 0

Hình vẽ minh họa

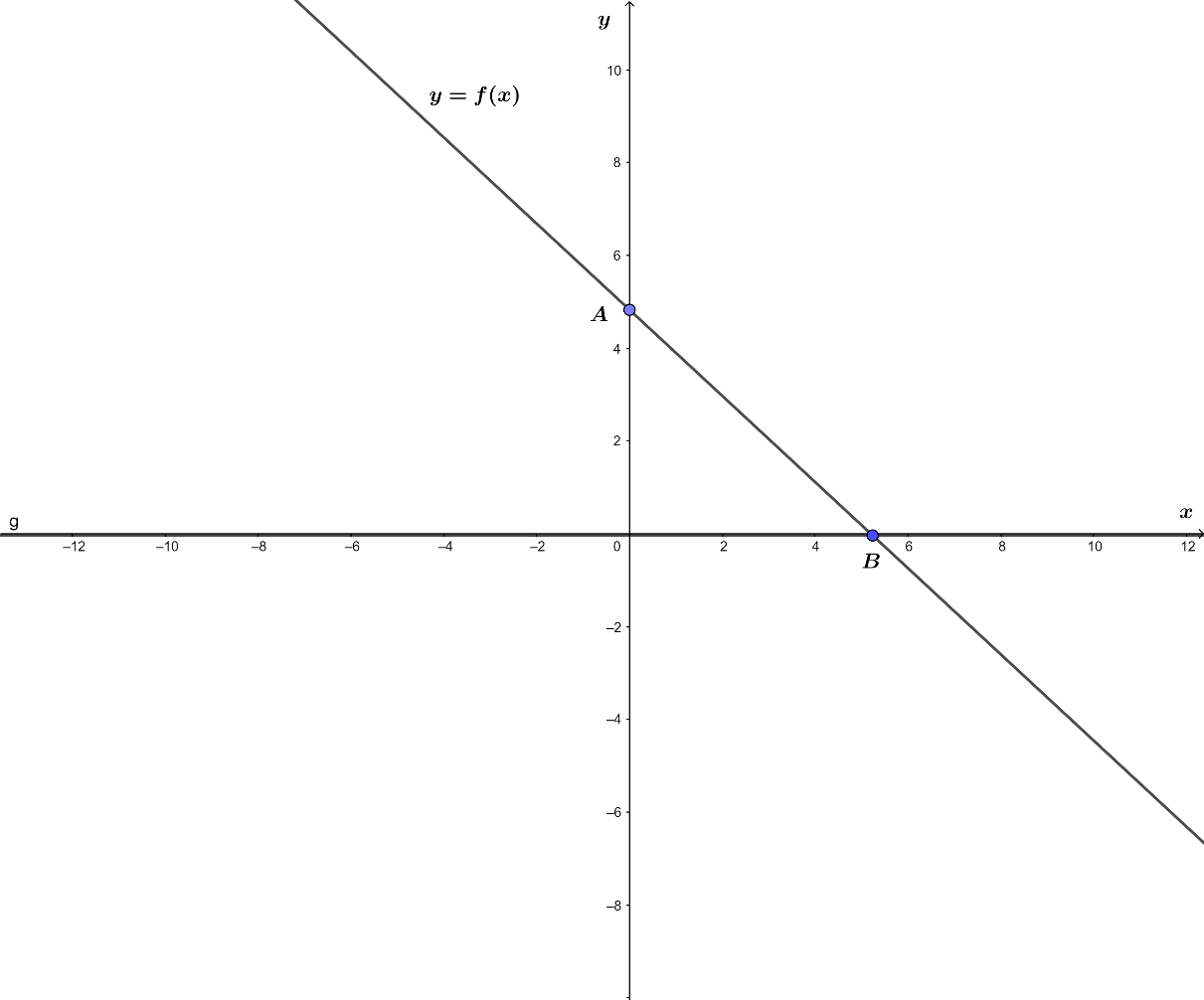
Tìm điều kiện để hàm số bậc nhất đồng biến nghịch biến

D. Xác định tính đồng biến, nghịch biến của hàm số bậc nhất

Ví dụ 1: Cho hàm số y = (m + 2)x + 3m. Tìm tất cả các giá trị của m để hàm số:

  1. Đồng biến trên \mathbb{R}
  2. Nghịch biến trên \mathbb{R}

Hướng dẫn giải

Hàm số đồng biến trên \mathbb{R} khi và chỉ khi m + 2 > 0 => m > -2

Hàm số nghịch biến trên \mathbb{R} khi và chỉ khi m + 2 < 0 => m < -2

Ví dụ 2: Cho hàm số: y = (1 – 3m)x + 3 + m đi qua điểm N(-1; 1). Hàm số đã cho đồng biến hay nghịch biến? Vì sao?

Hướng dẫn giải

Ta có hàm số y = (1 – 3m)x + 3 + m đi qua điểm N(-1; 1) => x = -1; y = 1. Thay tọa độ x, y vào hàm số đã cho ta được:

\begin{matrix} 1 = \left( {1 - 3m} \right).\left( { - 1} \right) + 3 + m \hfill \\ \Leftrightarrow m = \dfrac{{ - 3}}{4} \hfill \\ \Rightarrow y = \dfrac{{13}}{4}x + \dfrac{9}{4} \hfill \\ \end{matrix}

Dễ thấy \frac{{13}}{4} > 0. Vậy hàm số đồng biến trên \mathbb{R}

E. Bài tập tìm điều kiện để hàm số bậc nhất đồng biến, nghịch biến

Bài tập 1: Cho hàm số y = (2 – a) + a. Biết đồ thị hàm số đi qua điểm M(3; 1), hàm số đồng biến hay nghịch biến?

Bài tập 2: Cho hàm số y = \left( {1 - \sqrt 3 } \right)x - 3

a) Hàm số trên đồng biến hay nghịch biến trên \mathbb{R}? Vì sao?

b) Tính giá trị của hàm số khi x = \left( {1 + \sqrt 3 } \right)

Bài tập 3: Cho hàm số y = (2m – 3)x + 1

a) Tìm điều kiện của m để hàm số là hàm số bậc nhất

b) Tìm điều kiện của m để hàm số đồng biến, nghịch biến trên \mathbb{R}

---------------------------------------------

Hy vọng tài liệu Bài tập Toán 9: Tìm m để hàm số đồng biến nghịch biến sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết, bài tập Hàm số bậc nhất, từ đó vận dụng giải các bài toán Toán lớp 9 một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 9. Chúc các em học tốt.

Chia sẻ bởi: Thùy Chi
Mời bạn đánh giá!
  • Lượt xem: 871
Tìm thêm: Toán 9 Bài tập Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

Chủ đề liên quan

Mới nhất trong tuần