Giaitoan.com Toán 12 Toán 12 Chân trời sáng tạo

Khám phá 1 trang 19 Toán 12 tập 1 Chân trời sáng tạo Giải Toán 12 Chân trời sáng tạo Bài 3

Nội dung
  • 1 Đánh giá

Khám phá 1 trang 19 SGK Toán 12

Toán 12 Khám phá 1 trang 19 tập 1 trong bài Bài 3: Đường tiệm cận của đồ thị hàm số SGK Toán 12 Chân trời sáng tạo được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Khám phá 1 Toán 12 trang 19

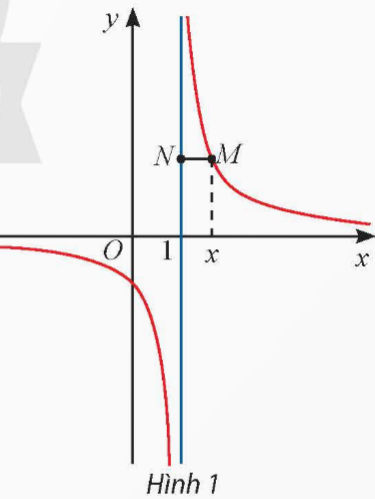
Khám phá 1 trang 19 toán 12 tập 1: Cho hàm số y = \frac{1}{x-1} có đồ thị như Hình 1.

a) Tìm \mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}

b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi x \to {1^ + } và x \to {1^ - }.

Lời giải chi tiết:

a) \mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}} =+\infty

\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}} =-\infty

b) Từ đồ thị ta có: M\left(x;\frac{1}{x-1}\right) và N\left(1;\frac{1}{x-1}\right)

⇒ MN\left(1-x;0\right)

⇒ MN=\sqrt{\left(1-x\right)^2}=x-1 (do x > 1)

Vậy khi x \to {1^ + } và x \to {1^ - } thì MN → 0.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Chân trời sáng tạo Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản

Chia sẻ bởi: Captain
Mời bạn đánh giá!
  • Lượt xem: 13
Tìm thêm: Toán 12 Toán 12 Chân trời sáng tạo
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần