Góc kề bù Bài tập Toán lớp 6
Bài tập Toán 6: Hai góc kề bù
Để trả lời cho các câu hỏi Thế nào là hai góc bù nhau, hai góc phụ nhau, hai góc kề bù? Tổng 2 góc kề bù bằng bao nhiêu độ?, ... GiaiToan.com giới thiệu đến thầy cô và học sinh tài liệu Bài tập Toán lớp 6: Góc kề bù. Tài liệu được xây dựng dựa theo trọng tâm chương trình Toán lớp 6 giúp các bạn học sinh củng cố, ôn tập kiến thức và định hướng tư duy làm bài tập cho các em học sinh. Mời thầy cô và các em học sinh cùng tham khảo tài liệu.
1. Hai góc kề nhau
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung.
Ví dụ minh họa:
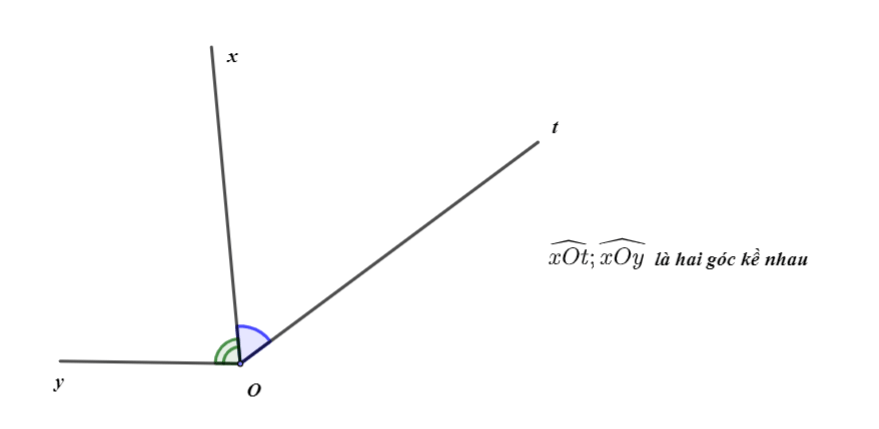
2. Hai góc phụ nhau
Hai góc phụ nhau là hai góc có tổng số đo bằng 90°
Ví dụ minh họa
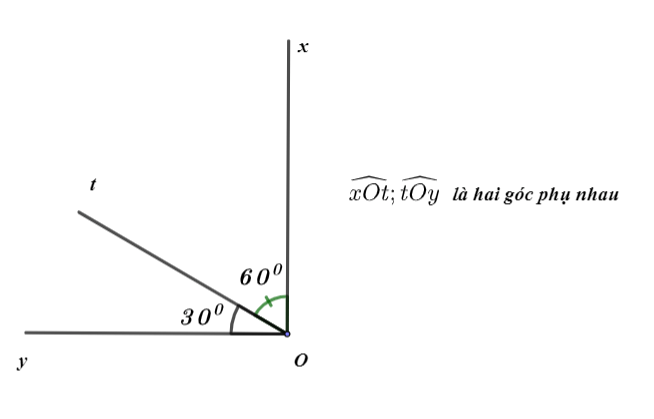
Ta có:

Vậy hai góc ![]() là hai góc phụ nhau
là hai góc phụ nhau
3. Hai góc bù nhau
Hai góc bù nhau là hai góc có tổng số đo bằng 180°
Ví dụ minh họa:
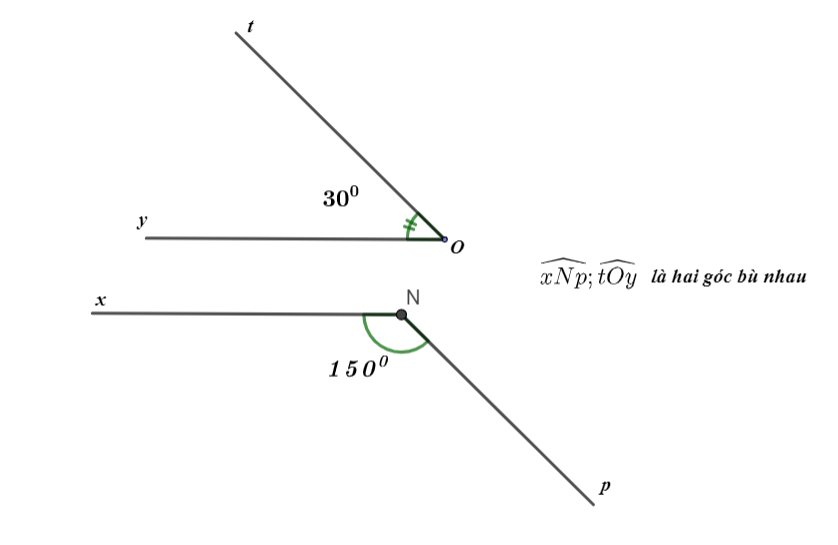
Ta có:

Vậy ![]() là hai góc bù nhau.
là hai góc bù nhau.
4. Hai góc kề bù
Hai góc được gọi là hai góc kề bù nếu như chúng vừa kề và vừa bù với nhau. Nghĩa là chúng có cạnh chung, hai cạnh tương ứng nằm ở hai phía mặt phẳng bờ là cạnh chung và tổng số đo của chúng là 1800
Ví dụ minh họa
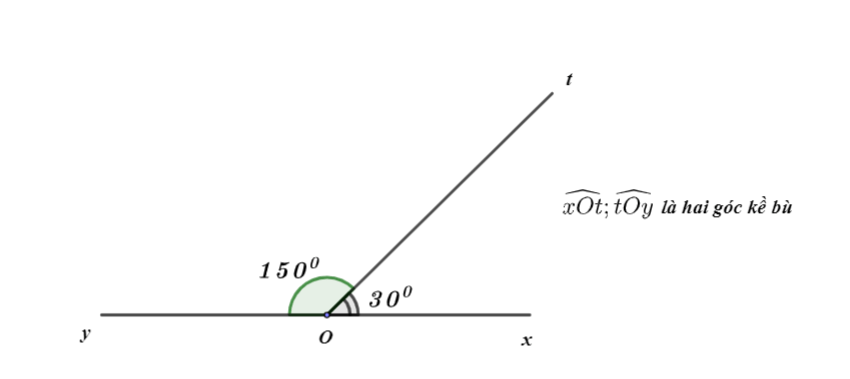
Ta có:

![]() là hai góc bù nhau. (1)
là hai góc bù nhau. (1)
Mà ![]() là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung.
là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung.
![]() là hai góc kề nhau (2)
là hai góc kề nhau (2)
Từ (1) và (2) ![]() là hai góc kề bù.
là hai góc kề bù.
5. Bài tập về hai góc kề nhau
Bài 1: Cho hai góc kề bù ![]() , biết
, biết ![]()
a. Tính số đo góc ![]()
b. Gọi Ot là tia phân giác của góc ![]() . Tính số đo góc
. Tính số đo góc ![]()
c. Gọi Op là tia phân giác của góc ![]() . Tính số đo góc
. Tính số đo góc ![]()
d. Góc ![]() là góc gì? Vì sao?
là góc gì? Vì sao?
Bài 2: Vẽ hai góc kề bù ![]() , biết
, biết ![]()
a. Tính số đo góc ![]()
b. Gọi Ot là tia phân giác của góc ![]() . Tính số đo góc
. Tính số đo góc ![]()
Bài 3: Cho hai tia Oz, Oy cùng nằm trên nửa mặt phẳng bờ chứa tia Ox. Biết ![]()
a. Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b. Tính số đo góc ![]()
Bài 4: Cho hai góc xOy và yOm là hai góc kề bù, biết góc xOy = 600
a. Tính số đo của góc yOm
b. Vẽ tia Oz là tia đối của tia Oy. Tính số đo của góc xOz
c. So sánh số đo góc yOm và góc xOz.
Bài 5: Cho bốn tia chung gốc O là Ox; Oy, Oz và Ot
a) Hỏi có bao nhiêu góc trong hình là những góc nào?
b) Nếu có hai tia (trong số bốn tia) là hai tia đối nhau thì có bao nhiêu góc trong hình vẽ? Là những góc nào?
Bài 6: Vẽ ba tia Ox, Oy, Oz chung gốc Ô, trong đó không có hai tia nào đối nhau. Hãy kể tên tất cả các loại hóc tạo bởi hai trong ba tia đó.
Bài 7: Cho ba điểm A, B, C không thẳng hàng. Điểm M nằm trong các góc BAC; ABC; ACB. Đường thẳng AM cắt BC tại D; đường thẳng BM cắt AC tại E; đường thẳng CM cắt AB tại F.
a) Điểm D thuộc miền trong của những góc nào trong hình vẽ.
b) Tìm trong hình vẽ những cặp góc kề bù nhau có đỉnh là M.
Bài 8: Trên cùng một nửa mặt phẳng bờ chứa tia OA kẻ hai tia OB và OC sao cho BOA = 1350, COA = 550. Tính số đo góc BOC
Bài 9: Cho aOb = 1000. Vẽ tia Oc sao cho bOc = 300
a) Có mấy cách vẽ hình
b) Tính số đo góc aOc trong từng cách vẽ.
Bài 10: Trên hai nửa mặt phẳng đối nhau bờ có chứa tia Oy vẽ tia Ox thuộc nửa mặt phẳng này thì tia Oz thuộc nửa mặt phẳng kia, sao cho xOz = 1200 và yOz = 1050. Tính số đo của xOz.
Bài 11: Trên đường thẳng a lấy các điểm M, N, P, Q sao cho điểm O nằm giữa hai điểm M và Q; điểm N nằm giữa hai điểm M và P. Từ điểm O ở ngoài đường thẳng a kẻ các tia OM, ON, OP và OQ. Biết MON = 200; NOP = 300; MOQ = 800. Tính số đo của MOP và POQ.
Bài 12: Cho ba điểm A, B, C không thẳng hàng. Kẻ các đường thẳng AB, AC, BC. Gọi M là điểm nằm trong góc ABC và góc ACB.
a) Chứng tỏ rằng cũng nằm trong góc BAC.
b) Gọi I là giao điểm của hai đường thẳng AM, BC. Hỏi điểm I nằm trong góc nào trong số các góc sau: ![]()
Bài 13: Vẽ hình theo cách diễn đạt sau:
a) Vẽ góc có đỉnh A, hai cạnh AB, AC. Điểm M nằm trong góc đó.
b) Vẽ góc xOy không phải góc bẹt.
c) Vẽ ba góc xOy, yOz, zOt sao cho tia Oz nằm trong góc xOy, tia Oy nằm trong góc zOt và góc xOt là góc bẹt.
-------------------------------------------------------------
Hy vọng tài liệu Hai góc kề bù mà GiaiToan đã giới thiệu trên đây sẽ giúp các em học thật tốt phần Hình học Toán lớp 6. Ngoài ra mời thầy cô và các em học sinh tham khảo thêm một số tài liệu: Giải Toán lớp 6, Luyện tập Toán lớp 6, Đề thi học kì 1 lớp 6, .... Chúc các em học tập tốt!
-------------------------------------------
Câu hỏi Toán lớp 6 liên quan:
- Khối lượng vitamin C trung bình trong một quả ớt chuông là 0,135 g, còn trong một quả cam là 0,045 g. Khối lượng vitamin C trong quả ớt chuông gấp bao nhiêu lần trong quả cam?
- Tính diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52cm
- Một căn phòng có dạng hình hộp chữ nhật với chiều dài 4,2 m, chiều rộng 3,5 m và chiều cao 3,2 m. Người ta muốn sơn lại trần nhà và bốn bức tường bên trong phòng. Biết rằng tổng diện tích các cửa là 5,4 m2.
- Một bác nông dân thu hoạch và mang cà chua ra chợ bán. Bác đã bán được 20 kg, ứng với số cà chua. Hỏi bác nông dân đã mang bao nhiêu kilôgam cà chua ra chợ bán?
- Giá niêm yết của một chiếc điện thoại di động là 625 nghìn đồng. Trong chương trình khuyến mại, mặt hàng này được giảm giá 10%. Như vậy, khi mua một chiếc điện thoại loại này người mua được giảm bao nhiêu tiền?
- Có bao nhiêu số tự nhiên chia hết cho 4 gồm 4 chữ số, chữ số tận cùng bằng 2
- Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1, chia cho 4 dư 2, chia cho 5 dư 3, chia cho 6 dư 4 và chia hết cho 11
- Tìm số tự nhiên khi chia cho 2,3,4,5 thì dư 2 và số đó là số lớn nhất có 3 chữ số
- Chứng minh A = 3^1 + 3^2 + 3^3 + … + 3^60 chia hết cho 13
- Chứng minh không có số tự nhiên nào chia cho 15 dư 6 và chia 9 dư 1
- Chứng minh 5 + 5^2 + 5^3 + . . . + 5^99 + 5^100 chia hết cho 6
- Có bao nhiêu số tự nhiên chia hết cho 4 gồm 4 chữ số, chữ số tận cùng bằng 2
- Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1, chia cho 4 dư 2, chia cho 5 dư 3, chia cho 6 dư 4 và chia hết cho 11
- Tìm số tự nhiên khi chia cho 2,3,4,5 thì dư 2 và số đó là số lớn nhất có 3 chữ số
- Chứng minh A = 3^1 + 3^2 + 3^3 + … + 3^60 chia hết cho 13
- Chứng minh không có số tự nhiên nào chia cho 15 dư 6 và chia 9 dư 1
- Chứng minh 5 + 5^2 + 5^3 + . . . + 5^99 + 5^100 chia hết cho 6
- Diện tích của 1 khu vườn hình chữ nhật có chiều rộng 25 m, chiều dài bằng 7/5 chiều rộng là bao nhiêu?
- Một khu vườn hình chữ nhật có diện tích 3600m² chiều rộng 40m, cửa ra vào của khu vườn rộng 5m. Người ta muốn làm hàng rào xung quanh vườn bằng 2 tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét thép gai để làm hàng rào?
- Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m, người ta phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở trong khu vực hình bình hành AMCN, cỏ sẽ trồng ở phần đất còn lại. Tiền công để trả cho mỗi mét vuông trồng hoa là 50 000 đồng, trồng cỏ là 40 000 đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
- Lượt tải: 190
- Lượt xem: 84.704
- Dung lượng: 221,4 KB








































