Giaitoan.com Toán 8

Đề khảo sát chất lượng đầu năm lớp 8 Đề thi khảo sát đầu năm lớp 8

Nội dung Tải về
  • 42 Đánh giá

Đề khảo sát chất lượng đầu năm lớp 8 - Có đáp án

Đề thi khảo sát chất lượng đầu năm lớp 8 môn Toán được GiaiToan.com biên soạn và đăng tải là tài liệu tham khảo hữu ích dành cho các em học sinh từ lớp 7 lên lớp 8, giúp các em ôn tập và hệ thống lại kiến thức môn Toán 8 hiệu quả. Đây là đề thi đã được chọn lọc nên có chất lượng cao, sẽ là đề kiểm tra năng lực bản thân rất tốt cho các bạn học sinh lớp 8. Mời các bạn tải về và thực hành.

I. Đề khảo sát chất lượng đầu năm Môn Toán lớp 8

A. Phần trắc nghiệm (4 điểm)

Chọn một phương án trả lời đúng trong các câu sau

Câu 1: Cho đa thức P = 7{x^2}y - 5x{y^2} + 3{x^2}y - y{x^2}, kết quả rút gọn của P là:

A. P = 10{x^2}y - 5x{y^2} - y{x^2}

B. P = - 9{x^2}y - 5x{y^2}

C. P = 7{x^2}y - 5x{y^2} + 3{x^2}y - y{x^2}

D. P = 7{x^2}y - 2x{y^2} - y{x^2}

Câu 2: Bậc của đơn thức \frac{1}{4}{x^2}y{z^3}

A. 2

B. 3

C. 5

D. 6

Câu 3: Ba độ dài nào dưới đây là độ dài ba cạnh của một tam giác:

A. 2cm, 6cm, 4cm

B. 2cm, 3cm, 4cm

C. 2cm, 3cm, 5cm

D. 1cm, 3cm, 5cm

Câu 4: Đơn thức nào dưới đây đồng dạng với đơn thức - 3{x^3}{y^2}z

A. - 3{x^2}{y^2}z

B. \frac{1}{3}{x^3}{y^2}z

C. 10{x^2}{y^3}z

D. {x^3}{y^2}{z^2}

Câu 5: Cho tam giác ABC có \widehat A = {90^0},\widehat B = {60^0} thì quan hệ giữa các cạnh trong tam giác ABC là:

A. AC < AB < BC

B. AC > AB > BC

C. AC < BC < AB

D. AB < AC < BC

Câu 6: x = 2 là nghiệm của đa thức nào sau đây?

A. {x^3} - 8

B. x - 1

C. 4 - x

D. {x^2} - 1

Câu 7: Cho tam giác ABC có AM là đường trung tuyến, G là trọng tâm tam giác. Chọn khẳng định đúng?

A. AG = \frac{1}{3}AM

B. MG = \frac{1}{3}AM

C. AG = 2MG

D. MG = \frac{2}{3}AG

Câu 8: Giá trị của biểu thức A = \frac{1}{2}{x^2} - 2x + 3 tại x = 2 là:

A. A = 2

B. A = 1

C. A = -2

D. A = -1

B. Phần Tự luận (6 điểm)

Câu 1: (2 điểm) Điểm kiểm tra môn Tiếng Anh của học sinh lớp 7A được cho trong bảng sau:

Điểm

3

4

5

6

7

8

9

10

Tần số

2

*

3

7

6

*

4

8

N = 40

a. Dấu hiệu cần tìm hiểu ở đây là gì?

b. Biết tần số điểm 4 và điểm 8 bằng nhau. Hoàn thành bảng số liệu?

c. Tính số trung bình cộng của dấu hiệu? Tìm Mốt của dấu hiệu?

Câu 2: (1,5 điểm) Cho đơn thức:

A = \left( {8{y^3}{x^2}} \right).\left( { - \frac{1}{2}{x^3}yz} \right),B = \left( {2{x^2}y} \right)\left( {\frac{{ - 1}}{{14}}{x^3}{y^3}z} \right)

a. Thu gọn đơn thức A, B

b. Chứng minh hai đơn thức trên đồng dạng.

Câu 3: (2 điểm) Cho các đa thức:

A(x) = 4x2 – 3x4 + 8 + 2x4 + x3 – 2x2

B(x) = x4 + 2x3 – 2x2 + 3x3 + x – 6

a. Thu gọn và sắp xếp các đa thức A(x) và B(x) theo lũy thừa giảm dần của biến.

b. Tìm hệ số bậc cao nhất, hệ số tự do, bậc của đa thức C(x) = A(x) – 2B(x).

Câu 4: (2,5 điểm) Cho tam giác ABC cân tại B \left( {\widehat B < {{90}^0}} \right). Kẻ AH vuông góc với BC , CK vuông góc với AB, M là giao điểm của AH và CK.

a) Chứng minh AH = CK

b) Chứng minh tam giác ACM cân.

c) Trên tia CK lấy điểm D sao cho DK = KC. Chứng minh \widehat {ADC} = \widehat {CAH}

Câu 5: Tìm giá trị nhỏ nhất của biểu thức:

T = |a - 2015| + |a - 2016| + |a - 2017|

II. Đáp án đề khảo sát chất lượng đầu năm

C. Đáp án phần trắc nghiệm

Câu 1.C

Câu 2.D

Câu 3.D

Câu 4.B

Câu 5.A

Câu 6.A

Câu 7.C

Câu 8.B

D. Đáp án phần tự luận

Câu 1:

a. Dấu hiệu: Điểm kiểm tra môn Tiếng Anh của học sinh lớp 7A.

b.

Điểm

3

4

5

6

7

8

9

10

Tần số

2

5

3

7

6

5

4

8

N = 40

c. Điểm trung bình: 7,025

Mốt của dấu hiệu: 10

Câu 2:

a. A = \left( {8{y^3}{x^2}} \right).\left( { - \frac{1}{2}{x^3}yz} \right)

A = \left[ {8.\left( { - \frac{1}{2}} \right)} \right].\left( {{x^2}.{x^3}} \right).\left( {y.{y^3}} \right).z

A = - 4.{x^{2 + 3}}.{y^{1 + 3}}.z

A = - 4{x^5}{y^4}z

B = \left( {2{x^2}y} \right)\left( {\frac{{ - 1}}{{14}}{x^3}{y^3}z} \right)

B = \left[ {2.\left( { - \frac{1}{{14}}} \right)} \right].\left( {{x^2}.{x^3}} \right).\left( {y.{y^3}} \right).z

B = \frac{{ - 1}}{7}.{x^{2 + 3}}.{y^{1 + 3}}.z

B = - \frac{1}{7}{x^5}{y^4}z

b. HS tự chứng minh

Câu 3:

a. Thu gọn và sắp xếp các đa thức A(x) và B(x) theo lũy thừa giảm dần của biến như sau:

Xét đa thức A(x)

A(x) = 4x2 – 3x4 + 8 + 2x4 + x3 – 2x2

A(x) = (4x2 – 2x2) + (-3x4 + 2x4) + x3 + 8

A(x) = 2x2 – x4 + x3 + 8

Sắp xếp đa thức A(x) theo lũy thừa giảm dần của biến:

A(x) = -x4 + x3 + 2x2 + 8

Xét đa thức B(x)

B(x) = x4 + 2x3 – 2x2 + 3x3 + x – 6

B(x) = x4 + (2x3 + 3x3) – 2x2 + x – 6

B(x) = x4 + 5x3 – 2x2 + x – 6

Sắp xếp đa thức B(x) theo lũy thừa giảm dần của biến:

B(x) = x4 + 5x3 – 2x2 + x - 6

b.  Ta có:

C(x) = A(x) – 2B(x)

C(x) = -x4 + x3 + 2x2 + 8 – 2(x4 + 5x3 – 2x2 + x – 6)

C(x) = -x4 + x3 + 2x2 + 8 – 2x4 – 10x3 + 4x2 – 2x + 12

C(x) = (-x4 – 2x4) + (x3 – 10x3) + (2x2 + 4x2) – 2x + 8 + 12

C(x) = -3x4 – 9x3 + 6x2 – 2x + 20

Câu 4:

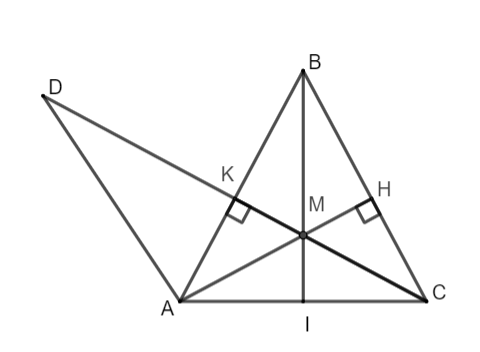
Đề khảo sát chất lượng đầu năm lớp 8

a. Chứng minh hai tam giác ABH và tam giác BKC bằng nhau (cạnh huyền - góc nhọn).

b. Suy ra từ câu a) cặp cạnh AM = MC (cặp cạnh tương ứng bằng nhau).

c. Ta có tam giác ACD có AK vừa là đường trung tuyến vừa là đường cao nên tam giác ADC cân tại A, kết hợp với hai góc ở đáy của tam giác MAC bằng nhau.

\Rightarrow \widehat {ADC} = \widehat {CAH}

Câu 5:

T = |a - 2015| + |a - 2016| + |a - 2017|

=> T = (|a - 2015| + |a - 2017|) + |a - 2016|

|a - 2015| + |a - 2017| ≥ | a - 2015 + 2017 - a| = 2

Dấu bằng xảy ra khi: 2015 \leqslant a \leqslant 2017 (*)

Ta lại có |a - 2016| ≥ 0 dấu bằng xảy ra khi x = 2016 (**)

Từ (*) và (**) ta có GTNN của T bằng 2

Dấu bằng xảy ra khi và chỉ khi x = 2016.

Mời các em, cùng quý phụ huynh tải miễn phí đề thi về và ôn luyện!

-----------------------------------------------------------

Hy vọng tài liệu Đề khảo sát chất lượng đầu năm môn Toán lớp 8 Có đáp án giúp sẽ giúp ích cho các bạn học sinh học nắm chắc cách giải hệ phương trình đồng thời học tốt môn Toán lớp 8. Chúc các bạn học tốt, mời các bạn tham khảo! Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 8, Lý thuyết Toán 8, Giải Toán 8, Luyện tập Toán 8, ...

Tài liệu liên quan:

Chia sẻ bởi: Thùy Chi
Mời bạn đánh giá!
  • Lượt tải: 924
  • Lượt xem: 30.057
  • Dung lượng: 365,6 KB
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán 8 Đề thi học kì 1 Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần