Chu vi và diện tích hình thang: Công thức và bài tập Công thức diện tích hình thang

41 Đánh giá

Chu vi, diện tích hình thang

1. Hình thang. Các dạng hình thang
- 1.1. Định nghĩa hình thang
- 1.2. Phân loại hình thang
2. Công thức tính chu vi hình thang
3. Công thức tính diện tích hình thang
- Bài thơ tính diện tích hình thang
4. Các dạng bài tập liên quan đến hình thang
5. Bài tập tính chu vi và diện tích hình thang

Hình bình thang: Công thức tính chu vi và diện tích là tài liệu do đội ngũ giáo viên của GiaiToan biên soạn với các công thức liên quan đến hình thang như tính chu vi, tính diện tích, tính đường cao,... giúp các bạn học sinh nắm vững các kiến thức về hình thang và áp dụng tính toán trong các bài tập. Mời các bạn học sinh cùng tham khảo bài viết.

1. Hình thang. Các dạng hình thang

1.1. Định nghĩa hình thang

Hình thang là một hình tứ giác có hai cạnh đối song song với nhau.

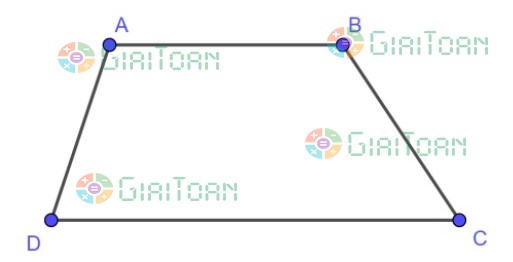
Chu vi và diện tích hình thang: Công thức và bài tập

Hình thang ABCD có:

• Cạnh đáy AB và cạnh đáy CD. Cạnh bên AD và cạnh bên BC

• Hai cạnh đáy là hai cạnh đối diện và song song nhau.

1.2. Phân loại hình thang

• Hình thang thường: là tứ giác có một cặp cạnh đối diện song song.

Chu vi và diện tích hình thang: Công thức và bài tập

• Hình thang vuông: là hình thang có hai góc vuông.

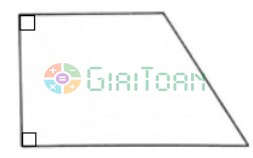
Chu vi và diện tích hình thang: Công thức và bài tập

• Hình thang cân (được học trong chương trình lớp 6 và lớp 8): là hình thang có hai cạnh bên bằng nhau.

Chu vi và diện tích hình thang: Công thức và bài tập

2. Công thức tính chu vi hình thang

✩ Chu vi hình thang được tính bằng tổng độ dài tất cả các cạnh của hình (tổng hai đáy và hai cạnh bên)

P = a + b + c + d

Trong đó: P: Chu vi hình thang

a, b, c, d: độ dài các cạnh của hình thang

3. Công thức tính diện tích hình thang

✩ Muốn tính diện tích hình thang, ta tính tổng hai đáy, nhân với chiều cao rồi chia cho 2.

S = (a + b) x h : 2

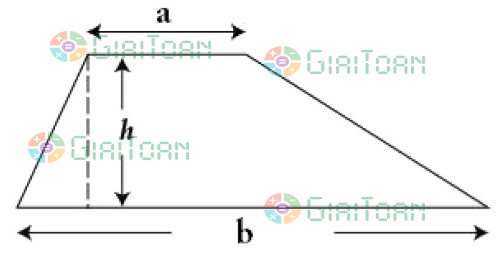
Trong đó: S là diện tích hình thang.

a, b là độ dài hai cạnh đáy.

h là đường cao.

Bài thơ tính diện tích hình thang

Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta mang cộng vào

Xong rồi nhân với chiều cao

Chia đôi lấy nửa thế nào chẳng ra.

4. Các dạng bài tập liên quan đến hình thang

Dạng 1: Tính chu vi hình bình thang khi viết độ dài các đáy và cạnh bên

Ví dụ 1: Tính chu vi của hình thang, biết đáy lớn bằng 12 cm; đáy bé bằng 10 cm và hai cạnh bên lần lượt bằng 7 cm và 8 cm

Lời giải chi tiết:

Chu vi hình thang là:

12 + 10 + 7 + 8 = 37 (cm)

Đáp số: 37 cm

Ví dụ 2: Hình thang cân có độ dài hai cạnh đáy và cạnh bên lần lượt là 40 m, 30 m và 25 m có chu vi là:

A. 95 m	B. 120 m
C. 2 875 m	D. 28 750 m

Lời giải chi tiết:

Chu vi của hình thang cân là

40 + 30 + (2 x 25) = 120 m

Đáp số: 120 m

Dạng 2: Tính độ dài cạnh bên của hình thang cân khi biết chu vi

Ví dụ 3: Tính độ dài của hình thang có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 68 cm và độ dài hai cạnh đáy lần lượt là 20 cm và 26 cm.

Lời giải chi tiết:

Tổng độ dài hai cạnh bên của hình thang là:

68 – 20 – 26 = 22 (cm)

Độ dài cạnh bên của hình thang là:

22 : 2 = 11 (cm)

Đáp số: 11 cm

Ví dụ 4: Một hình thang cân có chu vi bằng chu vi hình vuông cạnh 4 cm.

Độ dài hai đáy của hình thang cân là 3 cm, 5 cm.

Độ dài cạnh bên của hình thang cân đó là ... cm.

Lời giải chi tiết:

Chu vi của hình vuông cạnh 4 cm là:

4 x 4 = 16 (cm)

Độ dài hai cạnh bên của hình thang là:

16 – 5 – 3 = 8 (cm)

Hai cạnh bên bằng nhau

Độ dài cạnh bên là:

8 : 2 = 4 (cm)

Đáp số: 4 cm

Ví dụ 5: Cho hình thang cân có tổng hai đáy bằng 18 dm và chu vi hình thang cân 340 cm. Độ dài cạnh bên của hình thang cân là:

A. 8 cm	В. 16 dm
С. 8 dm	D. 16 cm

Lời giải chi tiết:

Đổi 340 cm = 34 dm.

Tổng độ dài hai cạnh bên là:

34 – 18 = 16 dm.

Vậy độ dài cạnh bên của hình thang cân là:

16 : 2 = 8 dm.

Đáp số: 8 dm

Dạng 3: Tính diện tích hình bình thang khi biết độ dài hai đáy và chiều cao

Ví dụ 6: Cho hình thang có độ dài đáy nhỏ bằng 5 cm, đáy lớn bằng 10 cm. Chiều cao của hình thang bằng 6 cm. Tính diện tích của hình thang đó.

Lời giải chi tiết:

Diện tích hình thang là:

(5 + 10) x 6 : 2 = 45 (cm²)

Đáp số: 45 cm²

Ví dụ 7: Tính diện tích và chu vi của hình thang cân có độ dài hai đáy là 4 cm và 10 cm; chiều cao 4 cm; cạnh bên 5 cm.

Lời giải chi tiết:

Diện tích hình thang đó là:

(4 + 10) : 2 x 4 = 28 (cm²)

Chu vi hình thang đó là:

4 + 10 + 5 x 2 = 24 (cm)

Đáp số: 24 cm

Dạng 4: Tính chiều cao khi biết độ dài hai đáy và diện tích

Ví dụ 8: Một hình thang vuông có diện tích bằng 14 dm², đáy bé bằng 2 dm và đáy lớn bằng 5 dm. Tính độ dài chiều cao của hình thang vuông đó.

Từ công thức tính diện tích hình thang, ta suy ra được công thức tính chiều cao của hình thang, đó là: h = S x 2 : (a + b) (Để tính chiều cao của hình thang, ta lấy diện tích chia cho trung bình cộng của hai đáy.)

Lời giải chi tiết:

Độ dài chiều cao của hình thang là:

14 x 2 : (2 + 5) = 4 (dm)

Đáp số: 4 dm

Dạng 5: Tính diện tích hình thang khi chưa biết độ dài hai đáy và chiều cao

Ví dụ 9: Một hình thang có chiều cao bằng 56 cm. Đáy lớn hơn đáy bé 24 cm và đáy bé bằng 2/5 đáy lớn. Tính diện tích của hình thang.

Lời giải chi tiết:

Hiệu số phần bằng nhau là:

5 – 2 = 3 (phần)

Độ dài đáy lớn là:

24 : 3 x 5 = 40 (cm)

Độ dài đáy bé là:

40 – 24 = 16 (cm)

Diện tích của hình thang là:

(16 + 40) x 56 : 2 = 1 568 (cm²)

Đáp số: 1 568 cm²

5. Bài tập tính chu vi và diện tích hình thang

Bài 1: Cho hình thang có hai cạnh đáy lần lượt là 6 cm và 4 cm. Chiều dài của cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?

Bài 2: Một hình thang có độ dài đáy lớn bằng 4,5 dm; độ dài đáy nhỏ bẳng 60 cm và chiều cao bằng 8 dm. Tính diện tích của hình thang đó.

Bài 3: Cho hình thang có đáy lớn bằng 10,5 cm; đáy nhỏ bằng 2/3 đáy lớn, chiều cao bằng 3,5 cm. Tính diện tích của hình thang đó.

Bài 4: Cho hình thang có tổng độ dài hai đáy là 45 cm và gấp 3 lần chiều cao, tính diện tích của hình thang đó.

Bài 5: Tính chiều cao của hình thang biết diện tích hình thang là 90 cm², đáy lớn bằng 5 dm, đáy bé bằng 1/2 đáy lớn.

Câu hỏi liên quan:

Tham khảo thêm công thức tính diện tích các hình:

-----------------------

Chia sẻ bởi: