Diện tích tam giác: Công thức và bài tập Công thức Toán

Công thức tính diện tích hình tam giác là tài liệu do đội ngũ giáo viên của GiaiToan biên soạn với các công thức tính diện tích hình tam giác giúp các bạn học sinh nắm vững các kiến thức và cách tính diện tích hình tam giác và áp dụng tính toán trong các bài tập. Mời các bạn học sinh cùng tham khảo bài viết.

1. Hình tam giác, định nghĩa hình tam giác

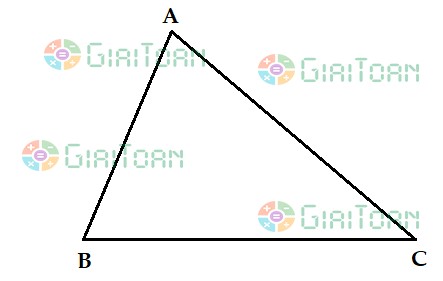
Hình tam giác ABC có:

+ Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.

+ Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C.

+ Ba góc là:

Góc đỉnh A, cạnh AB và AC

Góc đỉnh B, cạnh BA và BC

Góc đỉnh C, cạnh AC và CB

Phân loại hình tam giác

	Hình tam giác có ba góc nhọn
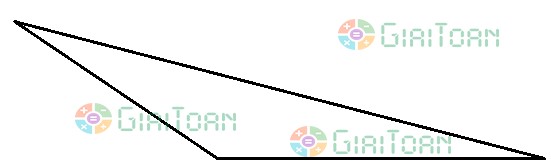	Hình tam giác có một góc tù và hai góc nhọn
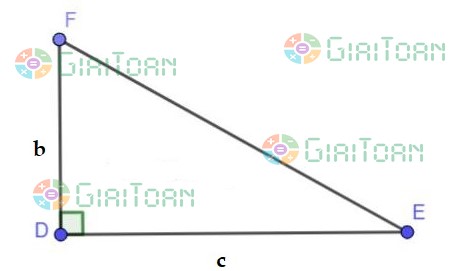	Hình tam giác có một góc vuông và hai góc nhọn

2. Công thức tính diện tích tam giác

✩ Muốn tính diện tích hình tam giác, ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

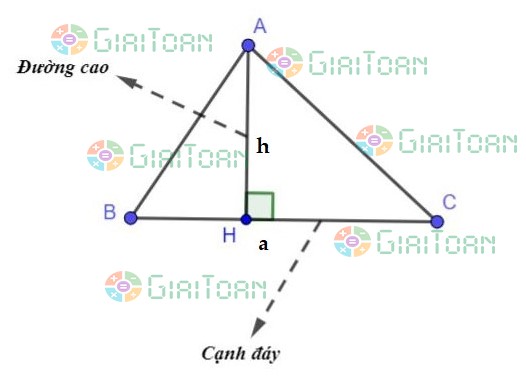
S = a x h : 2

Trong đó:

+ S là diện tích tam giác.

+ a là độ dài đáy.

+ h là đường cao.

✩ Muốn tính diện tích hình tam giác vuông, ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng đơn vị đo) rồi chia cho 2.

S = b x c : 2

Trong đó:

+ S là diện tích tam giác

+ b, c lần lượt là độ dài hai cạnh góc vuông của tam giác

Bài thơ tính diện tích hình tam giác

Diện tích tam giác sao ta

Chiều cao nhân đáy chia ra hai phần.

3. Các dạng bài tập liên quan đến diện tích hình tam giác

Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao

Ví dụ 1: Tính diện tích tam giác thường và tam giác vuông có:

a) Độ dài đáy bằng 32cm và chiều cao bằng 25cm.

b) Hai cạnh góc vuông có độ dài lần lượt là 3dm và 4dm.

Bài làm

a) Diện tích hình tam giác là:

32 x 25 : 2 = 400 (cm²)

b) Diện tích hình tam giác là:

3 x 4 : 2 = 6 (dm²)

Đáp số: a) 400cm²

b) 6dm²

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao

+ Từ công thức tính diện tích, ta suy ra công thức tính độ dài đáy: a = S x 2 : h

Ví dụ 1: Tính độ dài cạnh đáy của hình tam giác có chiều cao bằng 80cm và diện tích bằng 4800cm².

Bài làm

Độ dài cạnh đáy của hình tam giác là:

4800 x 2 : 80 = 120 (cm)

Đáp số: 120cm

Ví dụ 2: Cho hình tam giác có diện tích 5/8m² chiều cao là 1/2 m. Tính độ dài cạnh đáy của tam giác đó?

Để xem lời giải chi tiết của bài toán, mời nhấn vào đường link: Bài tập diện tích hình tam giác

Bài làm

Độ dài cạnh đáy của tam giác là:

(m)

Đáp số: 5/2m

Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy

+ Từ công thức tính diện tích, ta suy ra công thức tính chiều cao: h = S x 2 : a

Ví dụ 1: Tính chiều cao của hình tam giác có độ dài cạnh đáy bằng 50cm và diện tích bằng 1125cm².

Bài làm

Chiều cao của hình tam giác là:

1125 x 2 : 50 = 45 (cm)

Đáp số: 45cm

3. Bài tập tính diện tích tam giác

Tham khảo thêm các bài tập về tính diện tích hình tam giác: Bài tập diện tích hình tam giác

Bài 1: Tính diện tích của hình tam giác có chiều cao bằng 3dm và độ dài cạnh đáy bằng 5dm.

Bài 2: Một thửa ruộng hình tam giác có chiều dài cạnh đáy bằng 20m và chiều cao của thửa ruộng bằng 16m. Tính diện tích của thửa ruộng đó.

Bài 3: Tính diện tích hình tam giác vuông có độ dài hai cạnh góc vuông lần lượt là:

a) 35cm và 20cm.

b) 17dm và 14dm.

Bài 4: Tính độ dài cạnh đáy của hình tam giác có chiều cao bằng 50m và diện tích bằng 925m².

Bài 5: Một hình tam giác có cạnh đáy bằng 24m và diện tích bằng diện tích bằng diện tích một hình chữ nhật chiều dài 20m và chiều rộng 12m. Tính chiều cao hình tam giác ấy.

---------

Như vậy, GiaiToan.com đã gửi tới các bạn học sinh Công thức tính diện tích hình tam giác. Ngoài ra, các bạn học sinh có thể tham khảo thêm các tài liệu và các công thức khác khác do GiaiToan biên soạn để học tốt môn Toán hơn.