Bài 2 trang 36 Toán 12 tập 1 Chân trời sáng tạo Giải Toán 12 Chân trời sáng tạo Bài 4

Bài 2 trang 36 SGK Toán 12

Toán 12 Bài 2 trang 36 tập 1 trong bài Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản SGK Toán 12 Chân trời sáng tạo được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Bài 2 Toán 12 trang 36

Lời giải chi tiết:

a) Tập xác định của hàm số: .

Ta có: y' = 3x² - 6x

y'' = 6x - 6; y'' = 0 ⇔ x = 1.

=> Tọa độ điểm I(1; 0).

b) Ta có: y' = 0 ⇔ 3x² - 6x = 0

⇔ x = 0 hoặc x = 2.

Lập bảng biến thiên:

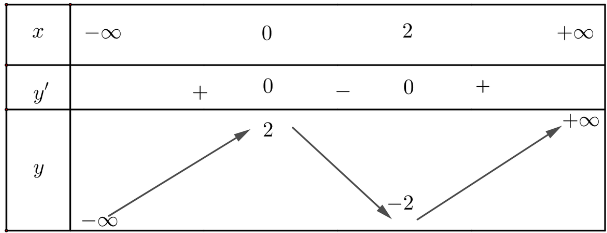
Hàm số đạt cực đại tại x = 0 và y_CĐ = 2

Hàm số đạt cực đại tại x = 2 và y_CT = - 2

Tọa độ trung điểm của đoạn thẳng nối hai cực trị là (1; 0).

Vậy I là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số

---> Câu hỏi cùng bài:

• Bài 3 trang 36 toán 12 tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:
• Bài 4 trang 36 toán 12 tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:
• Bài 5 trang 36 toán 12 tập 1: Cho hàm số:
• Bài 6 trang 36 toán 12 tập 1: Bạn Việt muốn dùng tấm bìa hình vuông cạnh 6 dm

-------> Bài tiếp theo: Giải Toán 12 Chân trời sáng tạo Bài tập cuối chương 1