Giaitoan.com Toán 8 Luyện tập Toán 8

Trường hợp đồng dạng thứ nhất của tam giác Luyện tập Toán 8

Nội dung
  • 1 Đánh giá

Tam giác đồng dạng

Chuyên đề Toán 8: Trường hợp đồng dạng thứ nhất của tam giác được biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các bạn học sinh ngoài bài tập trong sách giáo khoa (sgk) có thể luyện tập thêm các dạng bài tập cơ bản nhất để biết được cách giải các bài toán trường hơp đồng dạng cạnh - cạnh - cạnh. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán lớp 8. Các bạn học sinh có thể luyện tập nhằm củng cố thêm kiến thức lớp 8 của mình. Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

1. Cách chứng minh tam giác đồng dạng

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng

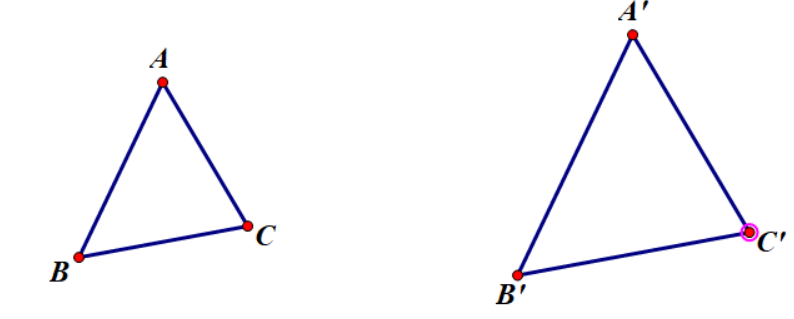
Xét tam giác ABC và A’B’C’ ta có:

\dfrac{{{A^\prime }{B^\prime }}}{{AB}} = \dfrac{{{A^\prime }{C^\prime }}}{{AC}} = \dfrac{{{C^\prime }{B^\prime }}}{{CB}}

\Rightarrow \Delta ABC đồng dạng với \Delta {A^\prime }{B^\prime }{C^\prime }

2. Bài tập tam giác đồng dạng có đáp án

Ví dụ 1: Hai tam giác sau có đồng dạng không nếu độ dài các cạnh của chúng bằng 8cm, 12 cm, 18 cm và 27 cm, 18cm, 12cm

Hướng dẫn giải

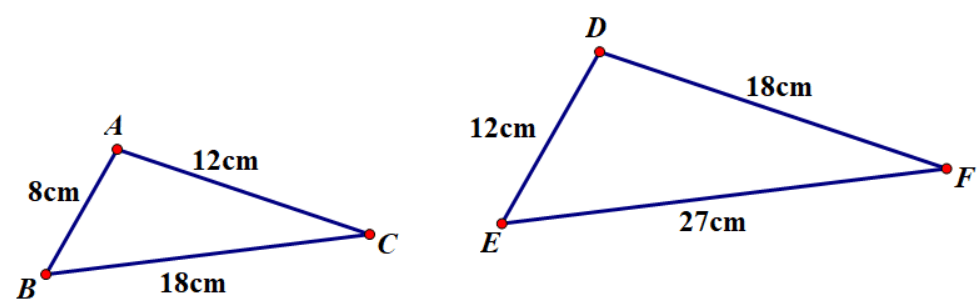
Gọi hai tam giác có độ dài các cạnh theo yêu cầu đề bài là \Delta ABC và \Delta DEF

Xét tam giác \Delta ABC  và \Delta DEF ta được:

\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{{CB}}{{EF}} = \dfrac{2}{3}

\Delta ABC đồng dạng  \Delta DEF (c – c – c)

Ví dụ 2: Tứ giác ABCD có AB = 4cm, BC = 20 cm, CD = 25cm, AD = 8cm, BD = 10cm. Tứ giác ABCD là hình gì?

Hướng dẫn giải

Xét \Delta ABD và \Delta BDC ta có:

\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{CD}} = \dfrac{2}{5}

\Delta ABD đồng dạng \Delta BDC  (c – c – c)

\Rightarrow \widehat {ABD} = \widehat {BDC} . Mà hai góc này ở vị trí so le trong nên AB // CD

\RightarrowABCD là hình thang

Ví dụ 3: Tam giác ABC có BC = a, AC = b, AB = c và . Chứng minh tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC

Hướng dẫn giải

Gọi độ dài ba đường cao kẻ từ A, B, C của làn lượt là {h_a};{h_b};{h_c}

Gọi là tam giác có độ dài các cạnh bằng độ dài ba đường cao của

Ta có: \dfrac{1}{2}a.{h_a} = \dfrac{1}{2}b.{h_b} = \dfrac{1}{2}c.{h_c}

\begin{array}{l} \Rightarrow a.{h_a} = b.{h_b} = c.{h_c}\\ \Rightarrow \dfrac{{a.{h_a}}}{{bc}} = \dfrac{{b.{h_b}}}{{bc}} = \dfrac{{c.{h_c}}}{{bc}} \end{array}

Mà bc = {a^2}nên \dfrac{{a.{h_a}}}{{{a^2}}} = \dfrac{{b.{h_b}}}{{{a^2}}} = \dfrac{{c.{h_c}}}{{{a^2}}}

\Rightarrow \frac{{{h_a}}}{a} = \dfrac{{{h_b}}}{c} = \dfrac{{{h_c}}}{b}

Xét  \Delta ABC và \Delta DEF có:

\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{{BC}}{{EF}}(vì \dfrac{{{h_a}}}{a} = \dfrac{{{h_b}}}{c} = \dfrac{{{h_c}}}{b}  )

\Delta ABC đồng dạng \Delta DEF  (c – c – c )

Vậy tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC

--------------------------------------------

Ngoài Trường hợp đồng dạng thứ nhất của tam giác môn Toán 8, các bạn có thể tham khảo thêm nhiều tài liệu ôn thi hay và chất lượng, các dạng toán nâng cao hay và khó. Qua đó giúp các bạn học sinh ôn tập, củng cố và nâng cao kiến thức Toán lớp 8.

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 156
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần