Giaitoan.com Toán 8 Luyện tập Toán 8

Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng Luyện tập Toán 8

Nội dung
  • 1 Đánh giá

Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng

Bài tập Toán 9: Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng là một dạng toán hình xuất hiện nhiều trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

1. Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng

- Nếu hai tam giác đồng dạng thì:

+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng

+ Tỉ số hai diện tích bằng bình phương tỉ số đồng dạng

2. Bài tập tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng

Ví dụ 1: Cho tam giác ABC. Qua điểm F nằm trong tam giác kẻ MN // BC, PQ // AB, IK // AC. Đặt diện tích tam giác ABC là S. Tìm vị trí của điểm F để tổng A = {S_{APFI}} + {S_{MBQF}} + {S_{CNFK}}đạt GTLN

Hướng dẫn giải

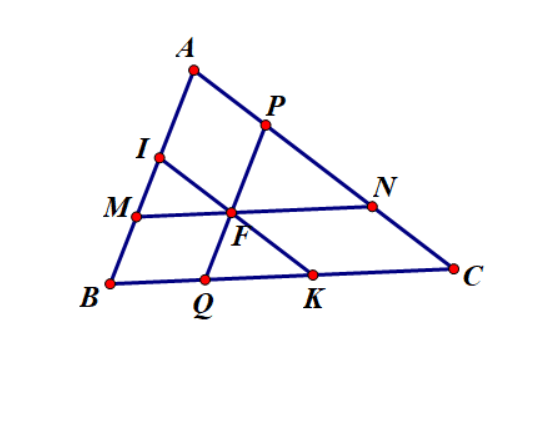
Đặt {S_{IMF}} = {a^2};\,{S_{PFN}} = {b^2};\,{S_{FQR}} = {c^2}\left( {a;b;c > 0} \right)

Ta có:\sqrt {{S_{ABC}}} = \sqrt {{S_{IMF}}} + \sqrt {{S_{FQK}}} + \sqrt {{S_{PFN}}}  . Hay {S_{ABC}} = {\left( {a + b + c} \right)^2}

\begin{array}{l} \Rightarrow {S_{APFI}} + {S_{MBQF}} + {S_{CNFK}} = 2{S_{ABC}} - \left( {{S_{MFI}} + {S_{PFN}} + {S_{FQK}}} \right)\\ \Rightarrow T = {\left( {a + b + c} \right)^2} - \left( {{a^2} + {b^2} + {c^2}} \right) \Rightarrow T = 2\left( {ab + bc + ca} \right) \le \dfrac{2}{3}{\left( {a + b + c} \right)^2} = \dfrac{2}{3}S\end{array}

Vậy T = \dfrac{2}{3}S khi a = b = c hay F là trọng tâm của tam giác ABC

Ví dụ 2: Cho tam giác ABC. Qua điểm F nằm trong tam giác kẻ MN // BC, PQ // AB, IK// AC. Biết rằng {S_{IMF}} = 9c{m^2};{S_{PFN}} = 16c{m^2};{S_{FQK}} = 25c{m^2} . Tính diện tính tam giác ABC

Hướng dẫn giải

Nhận thấy BMFQ, CNFK là hình bình hành

Ta có: \Delta FQKđồng dạng\Delta ABC  ; \Delta IMFđồng dạng \Delta ABC  ; \Delta PFNđồng dạng \Delta ABC

Thì :

\begin{array}{l} \dfrac{{\sqrt {{S_{IMF}}} }}{{\sqrt {{S_{ABC}}} }} = \dfrac{{MF}}{{BC}};\dfrac{{\sqrt {{S_{PQK}}} }}{{\sqrt {{S_{ABC}}} }} = \dfrac{{QK}}{{BC}};\dfrac{{\sqrt {{S_{PFN}}} }}{{\sqrt {{S_{ABC}}} }} = \dfrac{{NF}}{{BC}}\\ \Rightarrow \dfrac{{\sqrt {{S_{IMF}}} + \sqrt {{S_{PQK}}} + \sqrt {{S_{PFN}}} }}{{\sqrt {{S_{ABC}}} }} = \frac{{MF + QK + NF}}{{BC}}\\ \Rightarrow \sqrt {{S_{ABC}}} = \sqrt {{S_{IMF}}} + \sqrt {{S_{PQK}}} + \sqrt {{S_{PFN}}} = 3 + 4 + 5 = 12\\ \Rightarrow {S_{ABC}} = 144\left( {c{m^2}} \right) \end{array}

Ví dụ 2: Cho tam giác ABC cố định có các góc B, C nhọn và hình chữ nhật MNPQ thay đổi nhưng luôn có M, N trên cạnh BC còn P, Q lần lượt trên cạnh AC và AB. Xác định vị trị của các điểm P, Q sao cho hình chữ nhật MNPQ có diện tích lớn nhất

Hướng dẫn giải

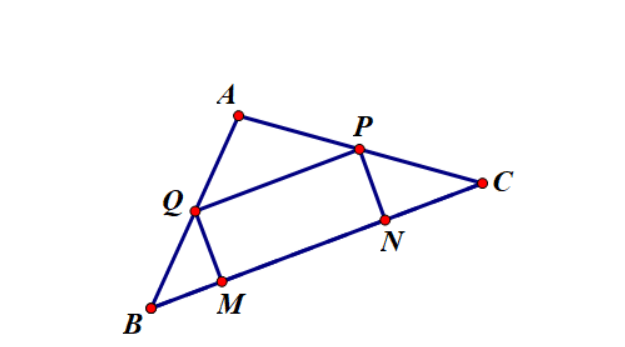
Gọi AH là đường cao của AB, AC cắt PQ tại I

Đặt BA = a; AH = h; PQ = x; MQ = y

Ta có: AI = h – y

Vì \Delta APQđồng dạng với  \Delta ACBnên

\begin{array}{l} \dfrac{{PQ}}{{BC}} = \dfrac{{AI}}{{AH}} \Leftrightarrow \dfrac{x}{a} = \dfrac{{h - y}}{h} \Rightarrow x = \dfrac{{a\left( {h - y} \right)}}{h}\\ \Rightarrow {S_{MNPQ}} = xy = \dfrac{a}{h}\left( {h - y} \right)y \end{array}

Vì a, h là các hằng số dương nên S lớn nhất khi (h – y ).y lớn nhất

Áp dụng hệ thức ab \le {\left( {\dfrac{{a + b}}{2}} \right)^2}

Ta có:\left( {h - y} \right)y \le {\left( {\dfrac{{h - y + y}}{2}} \right)^2} = \dfrac{{{h^2}}}{4} \Rightarrow {S_{MNPQ}} \le \dfrac{a}{h}.\frac{{{h^2}}}{4} = \dfrac{{ah}}{4}

Vậy GTLN của S là . Khi h – y = y \Leftrightarrow y = \dfrac{h}{2}

Ví dụ 3: Cho hình vuông ABCD, F là trung điểm của AD và E là trung điểm của FD. Các đường thẳng BE và CF cắt nhau tại G. Tính tỉ số diện tích của tam giác EFG với diện tích hình vuông ABCD

Hướng dẫn giải

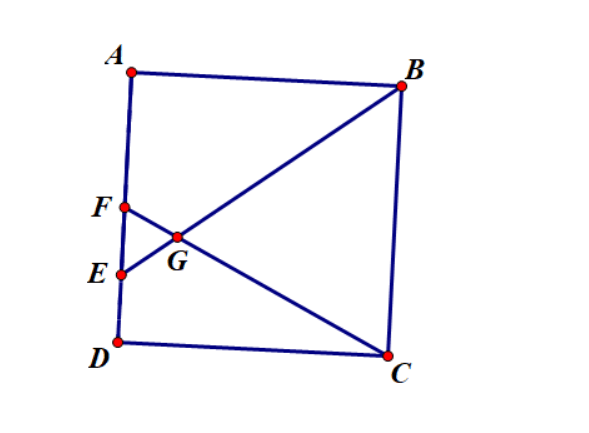
Vì ED = EF nên mà AF = 2 EF

Nên {S_{GAF}} = 2.{S_{EFG}}

Lại có:  \Delta GBCđồng dạng với \Delta GEF nên \dfrac{{{S_{GBC}}}}{{{S_{GEF}}}} = {\left( {\dfrac{{BC}}{{EF}}} \right)^2} \Rightarrow {S_{GBC}} = 16{S_{GEF}}

Do đó:{S_{GED}} + {S_{EFG}} + {S_{GBC}} = \left( {1 + 1 + 2 + 16} \right){S_{EFG}} = 20{S_{EFG}}

Mà {S_{GED}} + {S_{EFG}} + {S_{GAF}} + {S_{GBC}} = \dfrac{1}{2}{S_{ABCD}}

Vậy {S_{EFG}} = \dfrac{1}{{40}}{S_{ABCD}} \Rightarrow \dfrac{{{S_{EFG}}}}{{{S_{ABCD}}}} = \dfrac{1}{{40}}

Ví dụ 4: Cho tam giác ABC nhọn có AD, BE, CF là đường cao cắt nhau tại H. Chứng minh rằng \dfrac{{HB.HC}}{{AB.AC}} + \dfrac{{HA.HC}}{{CB.AB}} + \dfrac{{HB.HA}}{{CB.AC}} = 1

Hướng dẫn giải

Ta chứng minh được: \Delta CHE đồng dạng  \Delta CAF \Rightarrow \frac{{CH}}{{CA}} = \frac{{CE}}{{CF}}

Do đó:  \dfrac{{HB.HC}}{{AB.AC}} = \dfrac{{\frac{1}{2}HB.CE}}{{\dfrac{1}{2}CF.AB}} = \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}}

Tương tự ta có: \dfrac{{HA.HC}}{{CB.AB}} = = \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}};\dfrac{{HB.HA}}{{CB.AC}} = \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}}

Từ đó ta được \dfrac{{HB.HC}}{{AB.AC}} + \dfrac{{HA.HC}}{{CB.AB}} + \dfrac{{HB.HA}}{{CB.AC}} = \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = 1

Hy vọng tài liệu Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng sẽ giúp ích cho các bạn học sinh học nắm chắc kiến thức chuyên đề tam giác đồng dạng đồng thời học tốt môn Toán lớp 8. Chúc các bạn học tốt, mời các bạn tham khảo!

Ngoài ra mời quý thầy cô và học sinh tham khảo thêm một số nội dung:

Luyện tập Toán 8
Giải bài tập SGK Toán 8
Đề thi giữa học kì môn Toán 8

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 3.705
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần