Toán 10 bài 1: Hàm số Giải bài tập Toán 10 SGK

GiaiToan.com xin gửi tới bạn đọc bài viết Toán 10 bài 1: Hàm số để bạn đọc cùng tham khảo. Bài viết được chúng tôi biên soạn lời giải của các bài tập trong sách giáo khoa Toán 10 bài hàm số. Hi vọng đây là tài liệu hữu ích giúp bạn đọc học tập tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Trả lời câu hỏi Toán 10 Bài 1 trang 32

Hãy nêu một ví dụ cụ thể về hàm số.

Lời giải

Sự phụ thuộc về quãng đường đi được của 1 xe khách với vận tốc và thời gian.

Trả lời câu hỏi Toán 10 Bài 1 trang 33

Hãy chỉ ra các giá trị của hàm số trên tại x = 2001; 2004; 1999

Lời giải

x = 2001 ⇒ y = 375

x = 2004 ⇒ y = 564

x = 1999 ⇒ y = 339

Trả lời câu hỏi Toán 10 Bài 1 trang 34

Tìm tập xác định của các hàm số sau

a) g(x) =

b) h(x) =  

Lời giải:

a) Biểu thức g(x) = 3/(x + 2) xác định khi x + 2 ≠ 0 ⇔ x ≠ -2

TXĐ của hàm số là D = R\{-2}

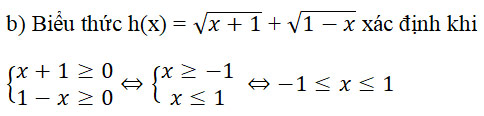
TXĐ của hàm số là D = [-1;1]

Trả lời câu hỏi Toán 10 Bài 1 trang 34

Tính giá trị của hàm số ở chú ý trên tại x = -2 và x = 5.

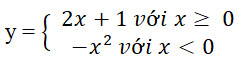
Lời giải

x = -2 ⇒ y = -(-2)² = -4

x = 5 ⇒ y = 2.5 + 1 = 11

Trả lời câu hỏi Toán 10 Bài 1 trang 35

Dựa vào đồ thị của hai hàm số đã cho trong hình 14

y = f(x) = x + 1 và y = g(x) = 1/2 x²

Hãy:

a) Tính f(-2), f(-1), f(0), f(2), g(-1), g(-2), g(0);

b) Tìm x, sao cho f(x) = 2;

Tìm x, sao cho g(x) = 2;

Lời giải

a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3

g(-1) = 0,5; g(-2) = 2; g(0) = 0

b) f(x) = 2 ⇒ x = 1

g(x) = 2 ⇒ x = 2 hoặc x = -2

Trả lời câu hỏi Toán 10 Bài 1 trang 38

Xét tính chẵn lẻ của các hàm số

a)y = 3x2 – 2; b) y = 1/x; c) y = √x

Lời giải

a) y = f(x) = 3x2 – 2

TXĐ:D = R ⇒ x ∈ D thì-x ∈ D

Ta có: f(-x) = 3(-x)2 – 2 = 3x2 – 2 = f(x)

Vậy hàm số y = f(x) = 3x2 – 2 là hàm số chẵn

b) y = f(x) = 1/x

TXĐ: D = R \{0} ⇒ x ∈ D thì-x ∈ D

f(-x) = 1/(-x) = -1/x = -f(x)

Vậy y = f(x) = 1/x là hàm số lẻ.

c) y = √x

TXĐ: D = [0; +∞) ⇒ x ∈ D thì -x ∉ D

Vậy hàm số trên không là hàm số chẵn cũng không là hàm số lẻ.

Bài 1 trang 38 SGK Toán 10

Tìm tập xác định của hàm số:

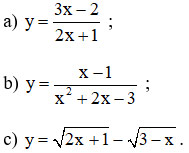
Lời giải:

a) y = có nghĩa khi 2x + 1 ≠ 0 ⇔ x ⇔ –1/2.

Vậy tập xác định của hàm y = là D = R \ {-1/2}.

b) y = xác định khi x2 + 2x – 3 ≠ 0.

Giải phương trình x2 + 2x - 3 = 0 ⇔ (x-1)(x+3) = 0 ⇔ x = 1 và x = -3

c) Do đó x2 + 2x – 3 ≠ 0 khi x ≠ 1 và x ≠ -3.

Vậy tập xác định của hàm số y = là D = R \ {1;-3}

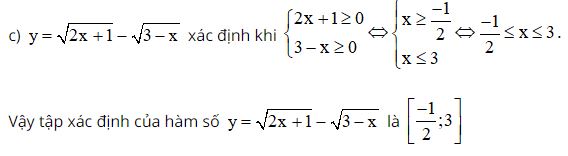
Bài 2 trang 38 SGK Toán 10

Cho hàm số

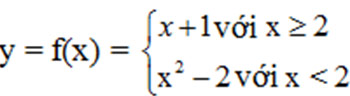
Tính giá trị của hàm số đó tại x = 3; x = -1; x = 2.

Lời giải:

- Ta có: x = 3 > 2 nên f(3) = 3 + 1 = 4.

- Ta có: x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.

- Ta có: x = 2 nên f(2) = 2 + 1 = 3.

Bài 3 trang 39 SGK Toán 10

Cho hàm số y = 3x2 - 2x + 1. Các điểm sau có thuộc đồ thị của hàm số không?

a) M(-1 ; 6)

b) N(1 ; 1)

c) P(0 ; 1)

Lời giải:

Tập xác định của hàm số y = f(x) = 3x² – 2x + 1 là D = R

a) Tại x = –1 thì y = 3.( –1)² – 2. (–1) + 1 = 3 + 2 + 1 = 6.

Vậy điểm M(–1; 6) thuộc đồ thị hàm số y = 3x² – 2x + 1.

b) Tại x = 1 thì y = 3.1² – 2.1 + 1 = 3 – 2 + 1 = 2 ≠ 1.

Vậy N(1; 1) không thuộc đồ thị hàm số.

c) Tại x = 0 thì y = 3.0² – 2.0 + 1 = 1.

Vậy điểm P(0 ; 1) thuộc đồ thị hàm số.

Bài 4 trang 39 SGK Toán 10

Xét tính chẵn lẻ của các hàm số sau:

a) y = |x|;

b) y = (x + 2)²;

c) y = x³ + x;

d) y = x² + x + 1.

Lời giải:

a) Đặt y = f(x) = |x|.

+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.

+ f(–x) = |–x| = |x| = f(x).

Vậy hàm số y = |x| là hàm số chẵn.

b) Đặt y = f(x) = (x + 2)².

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x + 2)² = (x – 2)² ≠ (x + 2)² = f(x)

+ f(–x) = (–x + 2)² = (x – 2)² ≠ – (x + 2)² = –f(x).

Vậy hàm số y = (x + 2)² không chẵn, không lẻ.

c) Đặt y = f(x) = x³ + x.

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x)³ + (–x) = –x³ – x = – (x³ + x) = –f(x)

Vậy y = x³ + x là một hàm số lẻ.

d) Đặt y = f(x) = x² + x + 1.

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ x² + x + 1 = f(x)

+ f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ –(x² + x + 1) = –f(x)

Vậy hàm số y = x² + x + 1 không chẵn, không lẻ.

Trên đây GiaiToan.com vừa gửi tới bạn đọc bài viết Toán 10 bài 1: Hàm số. Bài viết tổng hợp lời giải của 4 bài tập trong sách giáo khoa Toán 10. Mong rằng qua bài viết này bạn đọc có thể học tập tốt hơn môn Toán lớp 10 nhé. Chúc các bạn học tập thật tốt!