Bài 3.8 trang 42 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống Giải Toán 10 sách Kết nối tri thức

7 Đánh giá

Bài 3.8 trang 42 SGK Toán 10

Toán lớp 10 Bài 3.8 trang 42 là lời giải Hệ thức lượng trong tam giác SGK Toán 10 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 3.8 Toán 10 trang 42

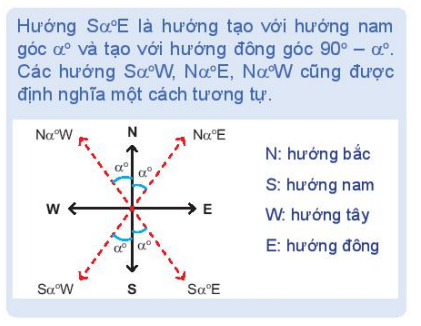
Bài 3.8 (SGK trang 42): Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70⁰E với vận tốc 70km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam theo vận tốc 8km/h. Sau 2 giờ kể từ khi bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng A tới nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Bài 3.8 trang 42 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

Hướng dẫn giải

Định lí cosin:

a² = b² + c² – 2bc.cosA

b² = a² + c² – 2ac.cosB

c² = a² + b² – 2ab.cosC

Định lí sin:

Trong tam giác ABC có: $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Lời giải chi tiết

Minh họa hướng đi của tàu bằng hình vẽ:

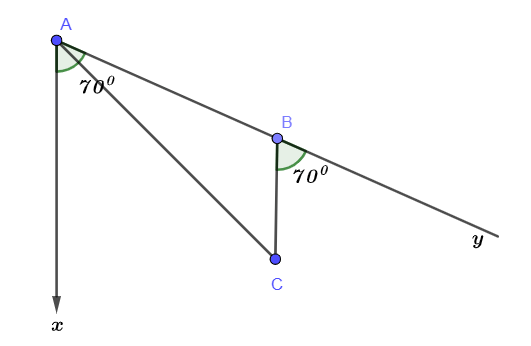
Bài 3.8 trang 42 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

a) Tàu cá xuất phát từ A đi theo hướng S70⁰E với vận tốc 70km/h trong 90 phút = 1,5 giờ thì tàu cá đi được đến B (vị trí tàu bị hỏng)

=> Quãng đường AB là: 70.1,5 = 105 (km)

Từ vị trí B tàu cá thả trôi với vận tốc 8km/h theo hướng nam sau 2h thì neo đậu vào đảo C

=> Quãng đường BC là: 8.2 = 16km

Khoảng cách từ cảng A đến nơi tàu neo đậu chính là đoạn AC.

Do tàu đi theo hướng S70⁰E nên phương AB hợp với phương nam Ax một góc 70⁰

=> $\widehat {xAB} = {70^0}$

Mà phương BC song song với phương nam Ax

=> $\widehat {CBx} = \widehat {xAB} = {70^0}$ (hai góc đồng vị)

=> $\widehat {ABC} = {110^0}$

Xét tam giác ABC ta có:

AC² = AB² + AC² – 2AB.AC.cosB

= 105² + 16² – 2.105.16.cos110⁰

= 12 430,19

=> AC = 111,49 km

Vậy khoảng cách từ cảng A đến nơi tàu neo đậu là 111,49 km.

b) Xét tam giác ABC, có:

$\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{{105}^2} + 111,{{49}^2} - {{16}^2}}}{{2.105.111,49}} \approx 0,99$

$\Rightarrow \widehat {BAC} \approx 7,{75^0}$

$\Rightarrow \widehat {xAC} = {70^0} - \widehat {BAC} = {70^0} - 7,{75^0} = 62,{25^0}$

Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62,25⁰E.

-----> Câu hỏi tiếp theo: Bài 3.9 trang 43 SGK Toán 10

---> Bài liên quan: Giải Toán 10 Bài 2 Hệ thức lượng trong tam giác

----------------------------------------

Trên đây là lời giải chi tiết Bài 3.8 Toán lớp 10 trang 42 Hệ thức lượng trong tam giác cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 3: Hệ thức lượng trong tam giác. Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: