Giaitoan.com Toán 8 Luyện tập Toán 8

Tính số đo góc của tứ giác Chuyên đề Toán 8

Nội dung
  • 1 Đánh giá

Bài tập Toán 8: Tứ giác

Chuyên đề Toán 8: Tổng các góc của một tứ giác đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh lớp 8 ôn tập và củng cố kiến thức về dạng toán về đơn thức, đa thức. Tài liệu bao gồm công thức, các dạng toán, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề tứ giác Toán lớp 8. Chúc các bạn học tập hiệu quả!

A. Cách tính số đo góc của tứ giác

Định lý: Tổng bốn góc của một tứ giác bằng 3600

=> Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.

Học sinh cần nhớ kiến thức: Hai góc bù nhau, hai góc phụ nhau.

Ví dụ: Tứ giác ABCD có \widehat A + \widehat B + \widehat C + \widehat D = {360^0}

B. Bài tập tính góc của tứ giác

Bài 1: Cho tứ giác ABCD có góc A trừ góc B bằng 400. Các tia phân giác góc C và góc D cắt nhau tại O. Biết góc \widehat {COD} = {110^0}. Chứng minh rằng AB \bot BC

Hướng dẫn giải

Hình vẽ minh họa:

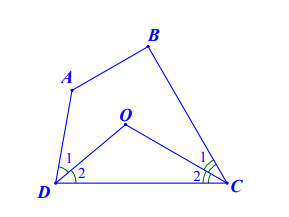
Tính số đo góc của tứ giác

Xét tam giác COD có

\widehat {COD} = {180^0} - \left( {\widehat {{C_2}} + \widehat {{D_2}}} \right) = {180^0} - \frac{{\widehat C + \widehat D}}{2}

Xét tứ giác ABCD có:

\widehat C + \widehat D = {360^0} - \left( {\widehat A + \widehat B} \right)

=> \widehat {COD} = {180^0} - \frac{{{{360}^0} - \left( {\widehat A + \widehat B} \right)}}{2} = {180^0} - {180^0} + \frac{{\widehat A + \widehat B}}{2}

Vậy \widehat {COD} = \frac{{\widehat A + \widehat B}}{2}

Theo bài ra ta có:

\widehat {COD} = {110^0} \Rightarrow \widehat A + \widehat B = {2.110^0} = {220^0}

Mặt khác \widehat A - \widehat B = {40^0} \Rightarrow \widehat B = \frac{{{{220}^0} - {{40}^0}}}{2} = {90^0}

=> AB \bot BC

Bài 2: Cho tứ giác ABCD có .\widehat A + \widehat B = {220^0} Các tia phân giác ngoài tại đỉnh C và D cắt nhau tại K. Tính dố đo của góc CKD.

Hướng dẫn giải

Hình vẽ minh họa:

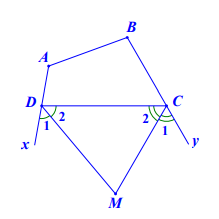
Tính số đo góc của tứ giác

Xét tứ giác ABCD có:

\widehat A + \widehat B = {360^0} - \left( {\widehat C + \widehat D} \right)

\begin{matrix} \widehat {CDx} + \widehat {DCy} \hfill \\ = \left( {{{180}^0} - \widehat D} \right) + \left( {{{180}^0} - \widehat C} \right) \hfill \\ = {360^0} - \left( {\widehat C + \widehat D} \right) \hfill \\ \end{matrix}

=> \widehat {CDx} + \widehat {DCy} = \widehat A + \widehat B = {220^0}

=> \frac{{\widehat {CDx} + \widehat {DCy}}}{2} = {110^0}

=> \widehat {{C_2}} + \widehat {{D_2}} = {110^0}

Xét tam giác CKD có: \widehat {CKD} = {180^0} - \left( {\widehat {{C_2}} + \widehat {{D_2}}} \right) = {180^0} - {110^0} = {70^0}

Bài 3: Tứ giác ABCD có . Chứng minh rằng các đường phân giác của góc B và góc D song song với nhau hoặc trùng nhau.

Hướng dẫn giải

Hình vẽ minh họa:

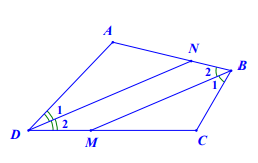
Tính số đo góc của tứ giác

Xét tứ giác ABCD có:

\widehat D + \widehat B = {360^0} - \left( {\widehat A + \widehat C} \right) = {360^0} - 2\widehat C

Vì \widehat {{B_2}} = \widehat {{B_1}};\widehat {{D_2}} = \widehat {{D_1}}

=> \widehat {{B_1}} + \widehat {{D_1}} = {180^0} - \widehat C

=> \widehat {{B_1}} + \widehat {{D_1}} + \widehat C = {180^0} (*)

Xét tam giác BCM có:

\widehat {{B_1}} + \widehat {{M_1}} + \widehat C = {180^0} (**)

TỪ (*) VÀ (**) suy ra:

=> DN //BM

Bài 4: Tứ giác ABCD có góc A bằng 1100, góc B bằng 1000. Các tia phân giác góc C và góc D cắt nhau tại E. Các đường phân giác của các góc ngoài tại C và D cắt nhau tại F. Tính \widehat {CEF};\widehat {CFD}.

Hướng dẫn giải

Hình vẽ minh họa:

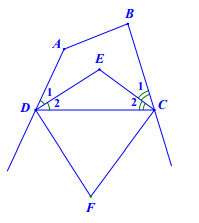
Tính số đo góc của tứ giác

Tứ giác ABCD có

\widehat C + \widehat D = {360^0} - \left( {\widehat A + \widehat B} \right)

= 3600 – 1100 – 1000 = 1500

=> \widehat {{C_1}} + \widehat {{D_1}} = \frac{{\widehat C + \widehat D}}{2} = {150^0}:2 = {75^0}

Xét tam giác CED có:

\widehat {CED} = {180^0} - \left( {\widehat {{C_1}} + \widehat {{D_1}}} \right) = {180^0} - {75^0} = {105^0}

VÌ DE và CF là các tia phân giác của hai góc kề bù nên DE vuông góc với DF. Tương tự chứng minh CE vuông góc với CF. Xét tứ giác CEDF có:

\widehat F = {360^0} - \widehat E - \widehat {ECF} - \widehat {EDF}

= 3600 – 1050 – 900 – 900 = 750

----------------------------------------------------

Hi vọng Chuyên đề Tứ giác là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 8 cũng như ôn luyện cho các kì thi sắp tới. Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 8, Lý thuyết Toán 8, Giải Toán 8, Luyện tập Toán 8, ... Chúc các bạn học tốt!

Chia sẻ bởi: Đội Trưởng Mỹ
Mời bạn đánh giá!
  • Lượt xem: 776
Tìm thêm: Toán 8 Chuyên đề Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần