Giaitoan.com Toán 8 Luyện tập Toán 8

Cách chứng minh hình thoi Bài tập Toán 8

Nội dung
  • 3 Đánh giá

Hình thoi - Toán 8

Chuyên đề Toán 8: Hình thoi được biên soạn giúp các bạn học sinh ngoài bài tập trong sách giáo khoa (sgk) có thể luyện tập thêm các dạng bài tập cơ bản nhất để biết được cách giải các bài toán chứng minh tứ giác là hình chữ nhật. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán lớp 8. Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

1. Hình thoi

Hình thoi là tứ giác có bốn cạnh bằng nhau

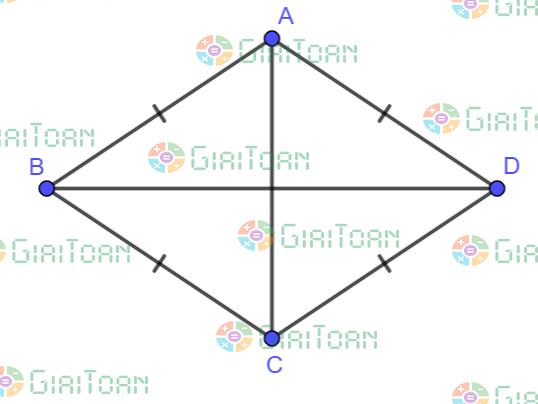
Cách chứng minh hình thoi

2. Tính chất hình thoi

Trong hình thoi:

a) Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường

b) Hai đường chéo là các đường phân giác của các góc của hình thoi

3. Dấu hiệu nhận biết hình thoi

– Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

– Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

– Hình bình hành có một đường chéo là phân giác một góc là hình thoi.

4. Chứng minh hình thoi

Ví dụ 1: Cho góc xOy và tia phân giác Ot. Từ điểm M thuộc Ot kẻ MA // Oy và MB // Ox (với A ∈ Ox; B ∈ Oy). Chứng minh tứ giác OAMB là hình thoi.

Hướng dẫn giải

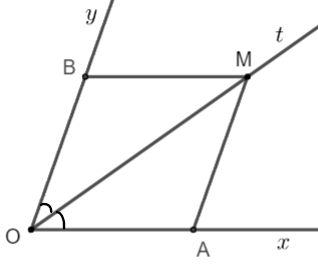
Xét tứ giác OAMB có MA // OB và MB // OA

Suy ra OAMB là hình bình hành (dấu hiệu nhận biết hình bình hành)

Mặt khác: OM là tia phân giác của góc AOB

Do đó OAMB là hình thoi (dhnb hình thoi).

Ví dụ 2: Cho hình bình hành ABCD có 2 đường cao AH = AK . Chứng minh ABCD là hình thoi.

Hướng dẫn giải

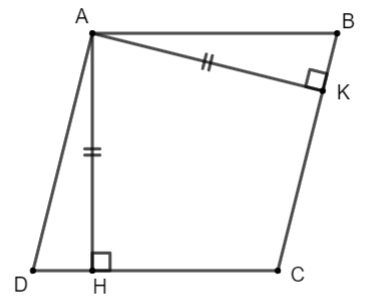
Ta có ABCD là hình bình hành nên \widehat{B}=\widehat{D}

Xét hai tam giác vuông ADH và AKB có \widehat{B}=\widehat{D} nên \widehat{HAD} = \widehat{KAB}

Xét tam giác ADH và tam giác ABK, ta có:

\widehat{AHD} =\widehat{AKB}=90^{\circ}

AH = AK (gt)

\widehat{HAD} = \widehat{KAB}

⇒ Δ ADH = Δ ABK (ch - gn)

⇒ AD = AB (hai cạnh tương ứng)

Xét hình bình hành ABCD có AD = AB (cmt)

Suy ra ABCD là hình thoi (dấu hiệu nhận biết)

5. Bài tập chứng minh hình thoi

Bài 1: Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi. 

Bài 2: Cho tam giác ABC cân tại A, gọi D là điểm đối xứng của A qua BC. Chứng minh ABDC là hình thoi.

Bài 3: Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.

a) Chứng minh tứ giác ABDC là hình thoi.

b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.

c) Chứng minh tứ giác AEMF là hình thoi.

Bài 4: Cho tam giác ABC cân tại A, đường cao AD. M là một điểm bất kì trên cạnh BC. Từ M vẽ ME vuông góc với AB tại E, MF vuông góc với AC tại F. Gọi I là trung điểm của AM.

a) Chứng minh tam giác EID và tam giác DIF cân

b) Tam giác ABC cần thêm điều kiện gì để tứ giác DEIF là hình thoi?

c) Với điều kiện của tam giác ABC ở câu b, gọi H là trực tâm của tam giác ABC. Chứng minh EF, ID, MH đồng quy.

------------------------------------------------------------

Mời bạn đọc tải tài liệu tham khảo đầy đủ!

Ngoài Các cách chứng minh hình thoi môn Toán 8, các bạn có thể tham khảo thêm nhiều tài liệu ôn thi hay và chất lượng, các dạng toán nâng cao hay và khó. Qua đó giúp các bạn học sinh ôn tập, củng cố và nâng cao kiến thức Toán lớp 8

Chia sẻ bởi: Người Nhện
Mời bạn đánh giá!
  • Lượt xem: 1.980
Tìm thêm: Toán 8 Chuyên đề Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần