Tính chất đường trung trực Đường trung trực

GiaiToan.com biên soạn và đăng tải tài liệu Tính chất đường trung trực bao gồm các kiến thức: định nghĩa đường trung trực, tính chất đường trung trực, tính chất ba đường trung trực trong tam giác, ... . Tài liệu được xây dựng dựa trên nội dung trọng tâm Toán hình 7 giúp học sinh củng cố lý thuyết và tính chất hình học của các đường trong tam giác. Mời các em học sinh cùng tham khảo.

1. Tính chất đường trung trực của một đoạn thẳng

- Đường trung trực của một đoạn thẳng là đường thẳng đi trung điểm và vuông góc với đoạn thẳng ấy.

Ví dụ: Cho đoạn thẳng AB, trung điểm C. d là đường thẳng trung trực của đoạn thẳng AB

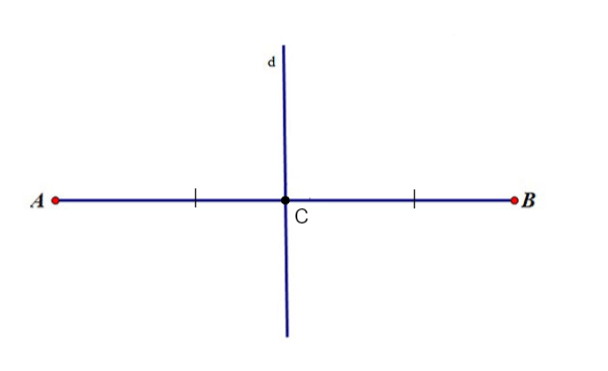Định lý 1: Điểm nằm trên đường trung trực thì cách đều hai mút của đoạn thẳng đó.

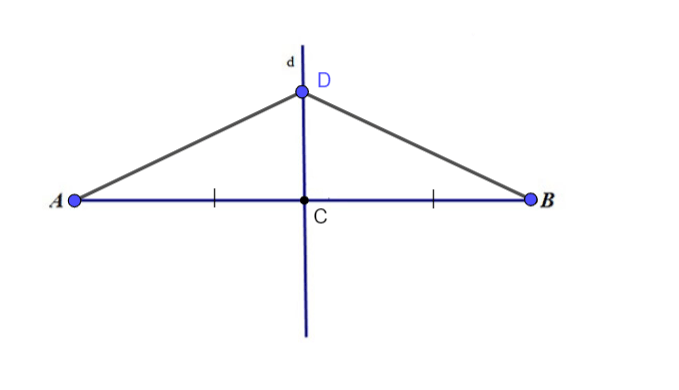
Ví dụ: d là đường trung trực của đoạn thẳng AB, D là một điểm nằm trên d => DA = DB

Định lý 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Ví dụ: DA = DB thì ta có thể xác định rằng M nằm trên đường trực của đoạn thẳng AB

2. Tính chất 3 đường trung trực của tam giác

Đường trung trực trong tam giác cân

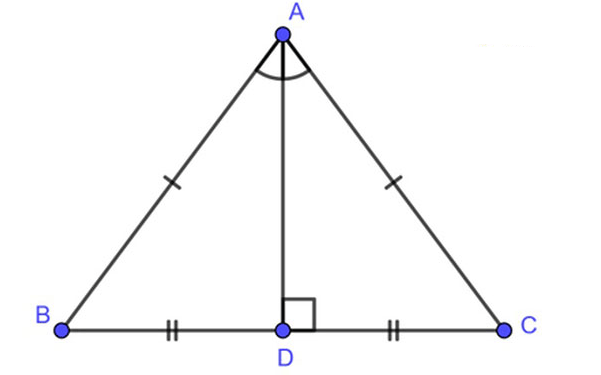
Định lý 1: Trong một tam giác cân đường trung trực của một cạnh đồng thời cũng sẽ là đường trung tuyến đối với cạnh đó.

Ví dụ: Cho tam giác ABC cân tại A, AD là đường trung trực của của cạnh BC đồng thời AD cũng là cũng là đường trung tuyến của cạnh BC.

Định lý 2: Nếu ba đường thẳng trung trực của một tam giác cùng đi qua một điểm thì điểm này sẽ cách đều 3 đỉnh của tam giác đó.

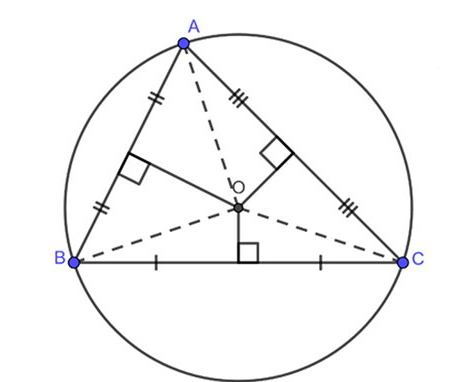
Ví dụ: Cho tam giác ABC, 3 đường trung trực của tam giác đều giao tại một điểm O

=> OA = OB = OC => Điểm O chính là tâm đường tròn ngoại tiếp của tam giác ABC

3. Các dạng bài toán thường gặp

a. Chứng minh đường trung trực

- Để có thể chứng minh d là đường trung trực của đoạn thẳng AB, ta chỉ cần chứng minh hai điểm A và chứa các điểm cách đều d hoặc sử dụng định nghĩa về tính chất đường trung trực để xác định.

b. Chứng minh hai đoạn thẳng bằng nhau

Định lý 3: Điểm nằm trên đường trung trực thì cách đều hai mút của đoạn thẳng đó.

c. Bài tập tính giá trị nhỏ nhất

Bước 1: Áp dụng tính chất đường trung trực để có thể thay đổi độ dài của một đoạn thẳng thành một con số chiều dài của một đoạn thẳng khác bằng nó.

Bước 2: Sử dụng bất đẳng thức của tam giác để tìm được giá trị nhỏ nhất.

d. Tâm đường tròn ngoại tiếp tam giác

Sử dụng tính chất giao điểm các đường trung trực của tam giác:

Định lý 4: Nếu ba đường thẳng trung trực của một tam giác cùng đi qua một điểm thì điểm này sẽ cách đều 3 đỉnh của tam giác đó. (Điểm đó là tâm đường trong ngoại tiếp tam giác)

e. Bài toán liên quan đến đường trung trực của một tam giác cân

- Để làm được dạng bài tập này, bạn nên chú ý rằng trong một cân đường trung trực cũng chính là đường trung tuyến, đường phân giác ứng với cạnh đáy.

f. Bài toán liên quan đến đường trung trực của một tam giác vuông

- Trong một tam giác vuông giao điểm của ba đường trung trực là trung điểm của cạnh huyền.

4. Bài tập Vận dụng tính chất đường trung trực

Bài 1: Cho 2 điểm A và B nằm trên cùng một mặt phảng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đường thẳng BC, AC cắt d tại E. Trên d lấy điểm M bất kỳ.

a) So sánh MA + MB và AC

b) Tìm vị trí của M trên d để MA + MB ngắn nhất

Bài 2: Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự ở D và E.

a) Các tam giác ABD, ACE là tam giác gì.

b) Đường tròn tâm O bán kính OA đi qua những điểm nào trên hình vẽ?

Bài 3: Cho tam giác ABC vuông tại A ,đương cao AH. Vẽ đường trung trục của cạnh AC cắt BC tai I và cát AC tai E.

a) Chứng minh IA = IB = IC.

b) Gọi M là trung điểm của đoạn AI, chứng minh MH = ME

c) BE cắt AI tại N, tính tỉ số của đoạn MN và AI

Bài 4: Cho 4 điểm A, B, C, D phân biệt. Với điều kiện nào sau đây thì đường thẳng AC là đường trung trực của đoạn thẳng BD ?

Bài 5: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, A = 5cm. Hỏi độ dài MB bằng ?

Bài 6: Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆AMN = ∆BMN

Bài 7: Cho ba tam giác ABC, DBC, EBC có chung đáy BC. Chứng minh 3 điểm A, D, E thẳng hàng

---------------------------------------------

Hy vọng tài liệu Toán 7 Đường trung trực sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết về các đường trong tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 7. Chúc các em học tốt.