Giaitoan.com Toán 7

Tính chất đường trung tuyến Toán 7 Công thức tính đường trung tuyến trong tam giác

Nội dung
  • 3 Đánh giá

Đường trung tuyến Toán 7

GiaiToan.com biên soạn và đăng tải tài liệu Tính chất đường trung tuyến bao gồm các kiến thức: định nghĩa đường trung tuyến trong tam giác, tính chất đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều và công thức tính độ dài đường trung tuyến trong tam giác, mời các em học sinh cùng tham khảo. Chúc các bạn học tập tốt!

1. Đường trung tuyến

- Đường trung tuyến của một tam giác là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện trong hình học phẳng.

+ Mỗi tam giác có 3 đường trung tuyến.

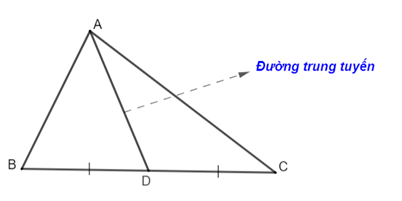
Tính chất đường trung tuyến Toán 7

2. Tính chất đường ba đường trung tuyến của tam giác

Tính chất 1: Ba đường trung tuyến của tam giác đồng quy tại một điểm được gọi là trọng tâm.

Tính chất 2: Khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng \frac{2}{3} đường trung tuyến tương ứng với đỉnh đó.

Tính chất 3: Khoảng cách từ trọng tâm đến trung điểm mỗi cạnh bằng \frac{1}{3} đường trung tuyến tương ứng với điểm đó.

Ví dụ minh họa: Cho tam giác ABC đường trung tuyến BE, CE, AD đồng quy tại điểm G.

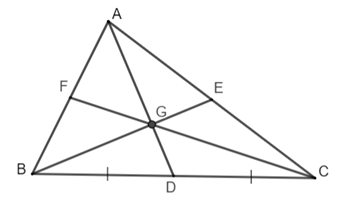Tính chất đường trung tuyến Toán 7

Tính chất 2: \frac{{AG}}{{AD}} = \frac{{BG}}{{BE}} = \frac{{CG}}{{CF}} = \frac{2}{3}

Tính chất 3: \frac{{GD}}{{AD}} = \frac{{GE}}{{BE}} = \frac{{GF}}{{CF}} = \frac{1}{3}

\Rightarrow \frac{{BG}}{{GE}} = \frac{{AG}}{{GD}} = \frac{{CG}}{{GF}} = 2

3. Tính chất đường trung tuyến trong tam giác vuông

- Đường trung tuyến của tam giác vuông sẽ có đầy đủ những tính chất của một đường trung tuyến tam giác.

Định lý 1: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

Ví dụ minh họa: Cho tam giác ABC vuông tại A, đường trung tuyến AD ứng với cạnh huyền.

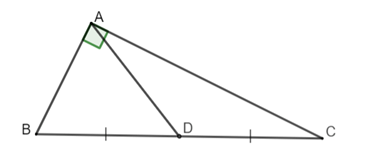Tính chất đường trung tuyến Toán 7

\Rightarrow AD = \frac{1}{2}BC

Hay AD = BD = CD

Định lý 2: Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Ngoài ra ta có tính chất đường trung tuyến trong tam giác cân:

- Định lý: Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy vừa là đường cao, đường trung trực và đường phân giác.

Bài tập ví dụ: Cho tam giác ABC cân tại A với đường trung tuyến AM, BC = 8cm, BN = 7,5 cm. Kẻ đường trung tuyến BN.

1. Chứng minh: ∆AMB = ∆AMC

2. Hãy tính độ dài đường trung tuyến AM.

Hướng dẫn giải

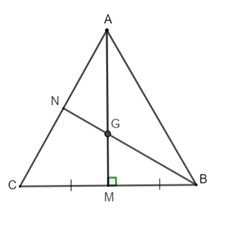Tính chất đường trung tuyến Toán 7

1. Xét tam giác AMB và tam giác AMC có:

AM là cạnh chung

MC = MB

AB = AC (∆ABC cân tại A)

⇒ ∆AMB = ∆AMC (c – c – c)

2. Gọi G là giao điểm của AM và BN

G là trọng tâm tam giác

\Rightarrow BG = \frac{2}{3}BN = \frac{2}{3}.7,5 = 5cm

Ta có: ∆ABC cân tại A

Mà AM là đường trung tuyến ⇒ AM là đường cao.

\Rightarrow \widehat {AMC} = \widehat {AMB} = {90^0}

Xét tam giác GMB vuông tại M, theo định lý Pi – ta – go ta có:

\begin{matrix} G{M^2} + M{B^2} = G{B^2} \hfill \\ \Rightarrow GM = \sqrt {G{B^2} - M{B^2}} = \sqrt {{5^2} - {4^2}} = 3cm \hfill \\ \end{matrix}

Mà GM = \frac{1}{3}AM \Rightarrow AM = 3.GM = 3.3 = 9cm

4. Bài tập luyện tập tính chất đường trung tuyến

Bài 1: Cho tam giác ABC cân tại A, kẻ đường trung tuyến AM, AB = AC = 10cm, BC = 12cm

a. Chứng minh ∆AMB = ∆AMC

b. Chứng minh AM vuông góc BC

c. Tính độ dài AM.

Bài 2: Cho tam giác ABC, đường trung tuyến AD. Vẽ đường trung tuyến BE cắt AD tại G. Gọi I và K lần lượt là trung điểm của GA và GB.

Chứng minh rằng:

1. IK // DE và IK = DE

2. AG = 2/3AD

Bài 3: Cho tam giác ABC có hai đường trung tuyến BD, CE cắt nhau tại G

a, Tính các tỉ số \frac{{BG}}{{BD}};\frac{{CG}}{{CE}}

b, Chứng minh BD + CE > \frac{3}{2}BC

---------------------------------------------

Hy vọng tài liệu Toán 7 Đường trung tuyến trong tam giác sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết về tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 7. Chúc các em học tốt.

Chia sẻ bởi: Bảo Bình
Mời bạn đánh giá!
  • Lượt xem: 847
Tìm thêm: Toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần