Giaitoan.com Toán 8 Luyện tập Toán 8

Tính chất đường phân giác của tam giác Luyện tập Toán 8

Nội dung
  • 1 Đánh giá

Tính chất đường phân giác của tam giác

Tính chất đường phân giác của tam giác đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh lớp 8 ôn tập và củng cố kiến thức về dạng toán 8. Tài liệu bao gồm các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đềTính chất đường phân giác của tam giác Toán lớp 8. Chúc các bạn học tập hiệu quả!

1. Tính chất đường phân giác của tam giác

– Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy

– Chú ý: Trong tam giác ABC, nếu D là điểm thuộc đoạn BC và thỏa mãn \dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}} thì AD là đường phân giác của góc A.

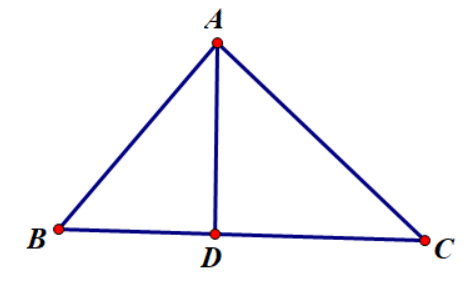
Xét tam giác ABC có AD là phân giác của \widehat {BAC} \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}

2. Bài tập tính chất đường phân giác trong tam giác

Ví dụ 1: Cho tam giác ABC, trung tuyến BM cắt tia phân giác CD tại P. Chứng minh rằng:

\dfrac{{PC}}{{PD}} - \dfrac{{AC}}{{BC}} = 1

Hướng dẫn giải

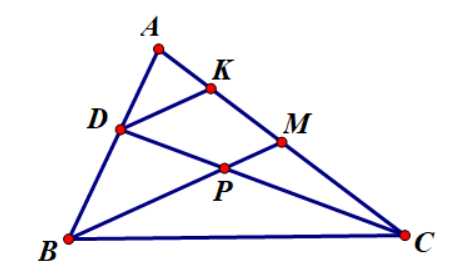
Ta có: \dfrac{{PC}}{{PD}} = \dfrac{{AC}}{{BC}} + 1

Do CD là phân giác của nên \dfrac{{DA}}{{DB}} = \dfrac{{AC}}{{BC}} \Leftrightarrow \dfrac{{DA}}{{DB}} + 1 = \dfrac{{AC}}{{BC}} + 1 \Leftrightarrow \dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{BC}} + 1

(1)

Vẽ DK // BM ( K thuộc AM) , theo định lý Ta- let ta có: \dfrac{{PC}}{{PD}} = \dfrac{{MC}}{{MK}} = \dfrac{{MA}}{{MK}} = \dfrac{{AB}}{{DB}}(2)

Từ (1) và (2) ta được \dfrac{{PC}}{{PD}} = \dfrac{{AC}}{{BC}} + 1(đpcm)

Ví dụ 2: Cho tam giác ABC cân tại A và \widehat A = {36^ \circ }. Chứng minh rằng:

AB2 = AB . BC + BC2

Hướng dẫn giải

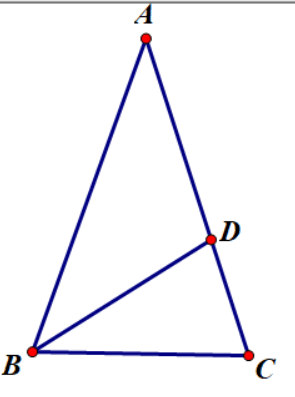
Kẻ phân giác BD của \widehat {ABC}, khi đó {\widehat B_1} = \widehat {{B_1}} = {36^ \circ } \Rightarrow \Delta ABD cân tại D và ∆ BCD cân tại B

Theo tính chất đường phân giác trong tam giác ABC, ta có:

\dfrac{{BA}}{{BC}} = \dfrac{{AD}}{{CD}} \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{BC}}{{AC - AD}}

Mà AB = AC; AD = BC nên

\begin{array}{l} \dfrac{{BA}}{{BC}} = \dfrac{{BC}}{{AB - BC}} \Leftrightarrow BA\left( {BA - BC} \right) = B{C^2}\\ \Leftrightarrow B{A^2} - BA.BC = B{C^2} \Leftrightarrow B{A^2} = BA.BC + B{C^2} \end{array}

Ví dụ 3: Cho tam giác ABCD có trọng tâm G và I là giao điểm của ba đường phân giác trong. Biết rằng IG // BC. Chứng minh rằng AB + AC = 2. BC

Hướng dẫn giải

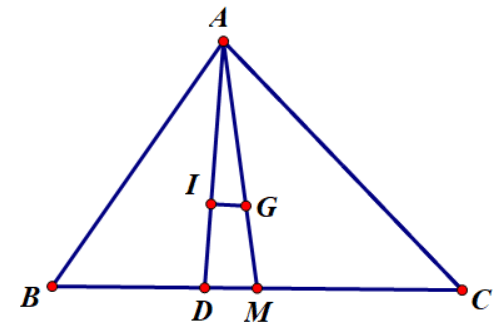
Gọi D, M lần lượt là giao điểm của AI, AG với BC

Theo tính chất đường phân giác trong của tam giác ABD, ACD. Ta có:

\dfrac{{IA}}{{ID}} = \dfrac{{AB}}{{BD}} = \dfrac{{CA}}{{CD}} = \dfrac{{AB + AC}}{{BD + CD}} = \dfrac{{AB + AC}}{{BC}}

Mà IG//BC \Rightarrow \dfrac{{IA}}{{ID}} = \dfrac{{GA}}{{GM}} = 2 \Rightarrow \dfrac{{AB + AC}}{{BC}} = 2

Hay AB + AC = 2. BC

Ví dụ 4: Cho tam giác ABCD có BE và CF là hai đường phân giác cắt nhau tại O. Chứng minh rằng nếuOB.OC = \frac{1}{2}BE.CF thì tam giác ABC vuông tại A

Hướng dẫn giải

Đặt BC = a, AC = b, AB = c

Theo tính chất đường phân giác, ta có:

\begin{array}{l} \dfrac{{BF}}{{FA}} = \dfrac{{BC}}{{AC}} \Rightarrow \dfrac{{BF}}{{FA + BF}} = \dfrac{{BC}}{{BC + AC}} = \dfrac{{BF}}{{AB}} = \dfrac{{BC}}{{BC + AC}}\\ \Rightarrow \dfrac{{BF}}{c} = \dfrac{a}{{a + b}} \Rightarrow BF = \dfrac{{ac}}{{a + b}} \end{array}

Lại có: \dfrac{{OF}}{{OC}} = \dfrac{{BF}}{{BC}} = \dfrac{c}{{a + b}} \Rightarrow \dfrac{{OF + OC}}{{OC}} = \dfrac{{a + b + c}}{{a + b}} \Rightarrow \dfrac{{CF}}{{OC}} = \dfrac{{a + b + c}}{{a + b}}

Tương tự ta có: \dfrac{{BE}}{{OB}} = \dfrac{{a + b + c}}{{a + b}}

Theo giả thiết ta có:

\begin{array}{l} BO.OC = \dfrac{1}{2}BE.CF \Rightarrow \dfrac{{BE.CF}}{{OB.OC}} = 2 \Rightarrow \dfrac{{{{\left( {a + b + c} \right)}^2}}}{{\left( {a + c} \right)\left( {a + b} \right)}} = 2\\ \Leftrightarrow {a^2} + {b^2} + {c^2} + 2ab + 2ac + 2bc = 2{a^2} + 2ab + 2ac + 2bc\\ \Leftrightarrow {a^2} + {b^2} = {c^2} \end{array}

Vậy tam giác ABC vuông tại A

3. Bài tập tự luyện

Bài 1: Tìm x trong các hình sau:

Bài 2: Cho tam giác ABC vuông tại A có AH là đường cao, BD là đường phân giác của góc ABC với D thuộc AC. AH cắt BD tại I

a) Tính tỉ số \frac{AI}{AB} và \frac{AD}{AB}

b) Chứng minh tam giác AID cân tại A

c) Chứng minh \frac{IH}{BH}=\frac{DC}{BC}

Bài 3: Cho tam giác ABC vuông tại A, đường phân giác của góc B cắt AC tại D. Từ D vẽ đường thẳng vuông góc với AC, đường thẳng này cắt BC tại E.

a) Chưng minh DC . AB = DA . CB

b) Chứng minh \frac{CB}{AB}=\frac{CE}{BE}

--------------------------------------------------------

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 19
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần