Giaitoan.com Toán 8 Luyện tập Toán 8

Cách chứng minh hình thang Bài tập Toán 8

Nội dung
  • 10 Đánh giá

Hình thang

Chuyên đề Toán 8: Hình thang được biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các bạn học sinh có thể luyện tập thêm các dạng bài tập cơ bản nhất để biết được cách giải các bài toán chứng minh tứ giác là hình thang. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán lớp 8. Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

1. Hình thang

– Hình thang là hình có hai cạnh đối song song

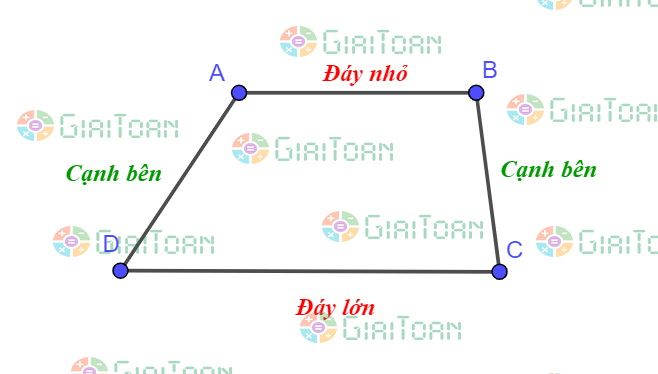
Cách chứng minh hình thang

– Hình thang cân là hình thang có hai góc kề một đáy bằng nhau

2. Tính chất hình thang cân

– Trong hình thang cân, hai cạnh bên bằng nhau

– Trong hình thang cân, hai đường chéo bằng nhau

3. Dấu hiệu nhận biết hình thang cân

– Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

4. Hình thang vuông

Hình thang vuông là hình thang có hai góc vuông

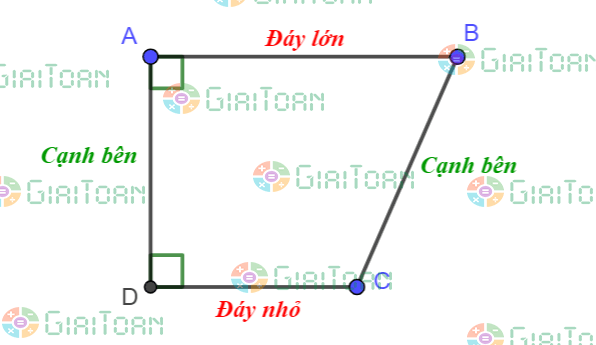
Cách chứng minh hình thang

5. Chứng minh hình thang

Ví dụ 1: Cho tứ giác ABCD có AD = CD, đường chéo AC là phân giác góc A. Chứng minh tứ giác ABCD là hình thang.

Hướng dẫn giải

Ta có: AD = CD suy ra tam giác ADC cân tại D

⇒\widehat {DCA} = \widehat {DAC}

Mà \widehat {DAC} = \widehat {BAC} (do AC là tia phân giác của góc A)

Suy ra \widehat {DCA} =\widehat {BAC}

Mà hai góc này ở vị trí so le trong

⇒ AB // CD

Vậy ABCD là hình thang.

Ví dụ 2: Cho tam giác ABC cân tại A có các đường trung tuyến BD và CE. Chứng minh BCDE là hình thang cân.

Hướng dẫn giải

Vì tam giác ABC cân tại A nên AB = AC.

Mà D là trung điểm của AC, E là trung điểm của AB nên AD = DC = AE = EB

Vì AD = AE nên tam giác ADE cân tại A, suy ra \widehat{ADE} =\widehat{AED} =\frac{180^{\circ}-\widehat{A} }{2}

Mạt khác, tam giác ABC cân tại A nên \widehat{ABC} =\widehat{ACB} =\frac{180^{\circ}-\widehat{A} }{2}

Suy ra \widehat{ADE} =\widehat{ACB}

Mà hai góc này ở vị trí đồng vị nên DE // BC

Suy ra BEDC là hình thang.

Lại có \widehat{EBC} =\widehat{DCB}

Suy ra BEDC là hình thang cân.

5. Bài tập chứng minh hình thang, hình thang vuông

Bài 1: Cho tam giác ABC vuông cân tại A. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tứ giác ABCD là hình gì? Vì sao?

Bài 2: Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chứng minh tứ giác ABCD là hình thang.

Bài 3: Cho tam giác ABC cân tại A có các đường cao BH và CK. Chứng minh BCHK là hình thang cân.

Bài 4: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.

a) Chứng minh BDEC là hình thang cân

b) Tính góc của hình thang cân đó, biết rằng góc A = 50o.

Bài 5: Cho hình thang cân ABCD (AD // BC và AD < BC). Gọi O là giao điểm của hai đường chéo hình thang cân. Chứng minh:

a) ∆ ACD = ∆ DBA

b) OA = OD

c) OB = OC

------------------------------------------------------------

Chia sẻ bởi: Phước Thịnh
Mời bạn đánh giá!
  • Lượt xem: 11.832
Tìm thêm: Toán 8 Chuyên đề Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần