Sự xác định đường tròn Đường tròn

Đường tròn Toán 9 được xem là dạng toán căn bản quan trọng trong chương trình Toán 9 và đề thi tuyển sinh vào lớp 10. Tài liệu dưới đây do đội ngũ GiaiToan.com biên soạn và chia sẻ giúp học sinh hiểu rõ hơn về các dạng toán đường tròn lớp 9. Qua đó giúp các bạn học sinh ôn tập và rèn luyện cho kì thi tuyển sinh vào lớp 10 sắp tới. Mời các bạn học sinh và quý thầy cô cùng tham khảo!

I. Đường tròn là gì?

Đường tròn tâm O bán kính R ( với R > 0) là hình gốm các điểm cách đều điểm O một khoảng không đổi bằng R

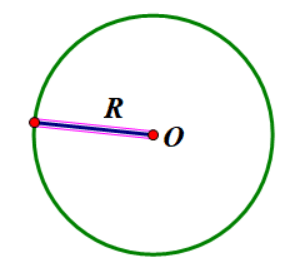
Đường tròn tâm O bán kính R được kí hiệu là (O; R), ta cũng có thể kí hiệu là (O) khi không cần chú ý đến bán kính

II. Cách xác định đường tròn

- Một đường tròn được xác định khi biết tâm và bán kính của nó

- Một đường tròn được xác định khi biết một đoạn thẳng là đường kính của đường tròn đó

- Qua ba điểm không thẳng hàng cho trước ta vẽ được một và chỉ một đường tròn

III. Cách chứng minh điểm thuộc đường tròn

- Chứng minh các điểm đó cùng cách đều một điểm O cố định. Khi đó các điểm đã cho cùng thuộc đường tròn tâm O

Hướng dẫn giải

Gọi O là trung điểm của BC (1)

AO là đường trung tuyến của tam giác ABC (2)

Từ (1) và (2) ta được

A, B, C cùng thuộc đường tròn (O)

Hướng dẫn giải

Xét tam giác DBC có:

NP là đường trung bình ( N là trung điểm BD, P là trung điểm DC

(1)

Xét tam giác DBC có:

MQ là đường trung bình ( M là trung điểm AB, Q là trung điểm AC)

(2)

Từ (1) và (2) ta được MNPQ là hình bình hành (*)

Lại có:

( đồng vị)

( đồng vị)

Mà

Lại có

(**)

Từ (*) và (**) ta được MNPQ là hình chữ nhật

Gọi O là giao điểm của MP và NQ , 4 điểm M, P, N, Q cùng thuộc 1 đường tròn

Hy vọng tài liệu tiếp tuyến sẽ giúp ích cho các bạn học sinh học nắm chắc lý thuyết về đường tròn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo! Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Lý thuyết Toán 9, Luyện tập Toán 9, Giải toán 9, ...