Giaitoan.com Toán 5 Toán nâng cao lớp 5

Một hình thang ABCD có tỉ số độ dài giữa đáy nhỏ AB và đáy lớn CD là 1/2 Toán nâng cao lớp 5 - Tỉ số

Nội dung
  • 1 Đánh giá

Bài toán về tỉ số và tỉ số phần trăm

Toán lớp 5: Giải toán về tỉ số phần trăm là tài liệu do GiaiToan biên soạn gồm các bài tập nâng cao và lời giải chi tiết về tỉ số và tỉ số phần trăm thường gặp. Mời các em tham khảo, luyện tập và củng cố kiến thức để chuẩn bị bước vào lớp 6.

Bài toán: Một hình thang ABCD có tỉ số độ dài giữa đáy nhỏ AB và đáy lớn CD là \frac{1}{2}. Hãy tính:

a) Tỉ số giữa diện tích tam giác ABC và ACD.

b) Tỉ số giữa độ dài đoạn OB và OD (O là giao điểm hai đường chéo).

Lời giải chi tiết:

Bài giải

a) Ta có: \frac{AB}{CD}=\frac{1}{2}

Hai tam giác ABC và ADC đều có đường cao là đường cao hình thang, có tỉ số hai đáy là \frac{1}{2} nên tỉ số diện tích của chúng là:

\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}AB.h}{\frac{1}{2}DC.h}=\frac{1}{2}

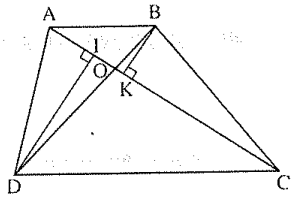
b) Kẻ BK và DI cùng vuông góc với AC.

+) Hai tam giác ABC và ADC có chung đáy là AC và có tỉ số diện tích bằng \frac{1}{2} nên tỉ số hai đường cao BK và DI cũng bằng \frac{1}{2}, hay \frac{BK}{DI}=\frac{1}{2}

+) Hai tam giác OAB và OAD có chung đáy là AO và có tỉ số hai đường cao BK và DI bằng \frac{1}{2} nên tỉ số diện tích hai tam giác cùng bằng \frac{1}{2}, hay \frac{S_{OAB}}{S_{OAD}}=\frac{1}{2}

+) Hai tam giác OAB và OAD có chung đường cao kẻ từ A xuống DB nên tỉ số giữa OB và OD bằng tỉ số diện tích giữa chúng:

\frac{OB}{OD}=\frac{1}{2}

--------------------------------------------

Tham khảo thêm:

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 09
Tìm thêm: Toán lớp 5 Toán nâng cao lớp 5
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần