Bài Toán Hai Tỉ Số Toán nâng cao lớp 4, 5

18 Đánh giá

Chuyên đề bài toán hai tỉ số được GiaiToan sưu tầm và đăng tải. Bài học bao gồm lý thuyết, phân loại dạng toán và các dạng bài tập tự luyện cho các em học sinh tham khảo, rèn luyện kỹ năng giải Toán 5, ôn tập chương 1 Toán 5. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

A. Lý thuyết bài toán hai tỉ số

Bài toán hai tỉ số là phần kiến thức nâng cao của hai dạng toán: Tìm hai số khi biết tổng và tỉ số của chúng; Tìm hai số khi biết hiệu và tỉ số của chúng đã được các em học sinh học trong chương trình lớp 4.

Tuy nhiên bài toán lại không hề cho chúng ta tổng hay hiệu của hai số để có thể sử dụng hai dạng toán trên.

Ngược lại, bài toán đưa ra tỉ số của hai đại lượng ở các thời điểm khác nhau, yêu cầu các em học sinh tận dụng sự chênh lệch đó để giải quyết đề bài.

Nhìn chung, bài toán hai tỉ số được chia làm 3 loại chính

Loại 1: Tổng hai số không thay đổi.
Loại 2: Hiệu hai số không thay đổi.
Loại 3: Một trong hai đại lượng không thay đổi.

Chúng ta cùng đi tìm hiểu về 3 loại này để chinh phục dạng toán hai tỉ số nhé.

B. Bài tập hai tỉ số

1. Tổng hai số không thay đổi

a) Ví dụ minh họa: Một hình chữ nhật có chiều dài bằng $\frac{3}{2}$ chiều rộng. Nếu tăng chiều rộng lên 5m và giảm chiều dài đi 5m thì chiều dài bằng $\frac{2}{3}$ chiều rộng. Tính diện tích của hình chữ nhật ban đầu.

Nhận xét: Bài toán cho tỉ số giữa chiều dài và chiều rộng nhưng không hề cho tổng hay hiệu độ dài của hai chiều dẫn đến ta không thể giải theo dạng toán tổng tỉ và hiệu tỉ thông thường.

Quan sát kĩ đề bài, các em học sinh nhận ra khi tăng chiều rộng lên 5m và giảm chiều dài đi 5m thì tổng độ dài của chiều rộng và chiều dài không thay đổi. Vậy chúng ta sẽ so sánh các đại lượng này với tổng độ dài (nửa chu vi)

Bài giải

Vì nửa chu vi của hình chữ nhật không thay đổi nên ta chọn nửa chu vi làm đơn vị.

Chiều rộng ban đầu so với nửa chu vi là: $\frac{2}{3+2}=\frac{2}{5}$ (nửa chu vi)

Chiều rộng sau khi tăng thêm 5m so với nửa chu vi là: $\frac{3}{2+3}=\frac{3}{5}$ (nửa chu vi)

Phân số chỉ 5m là:

$\frac{3}{5}-\frac{2}{5}=\frac{1}{5}$ (nửa chu vi)

Nửa chu vi của hình chữ nhật là:

5 x 5 = 25 (m)

Đến đây các em học sinh có thể thấy bài toán đã được đơn giản hóa về dạng tìm hai số khi biết tổng và tỉ số của chúng.

Chiều rộng ban đầu là:

25 : (2 + 3) x 2 = 10 (m)

Chiều dài ban đầu là:

25 - 10 = 15 (m)

Diện tích của hình chữ nhật ban đầu là:

15 x 10 = 150 $(m^2)$

Đáp số: 150 $m^2$

b) Bài tập

Bài 1: Một lớp học có số học sinh nam gấp 2 lần số học sinh nữ. Nếu giảm 4 học sinh nam đi và tăng 4 học sinh nữ lên thì số học sinh nam lúc này bằng $\frac{16}{11}$ số học sinh nữ. Tính số học sinh nữ ban đầu.

Nhận xét: Nếu giảm 4 học sinh nam đi và tăng 4 học sinh nữ lên thì tổng số học sinh sẽ không thay đổi.

Bài giải

Vì tổng số học sinh cả lớp không thay đổi nên ta chọn tổng số học sinh làm đơn vị

Ban đầu, số học sinh nam so với số học sinh cả lớp là: $\frac{2}{2+1}=\frac{2}{3}$ (tổng số học sinh)

Sau khi giảm đi 4 học sinh, số học sinh nam so với số học sinh cả lớp là: $\frac{16}{16+11}=\frac{16}{27}$ (tổng số học sinh)

Phân số chỉ 4 học sinh là: $\frac{2}{3}-\frac{16}{27}=\frac{2}{27}$ (tổng số học sinh)

Tổng số học sinh của lớp là:

$4:\frac{2}{27}=54$ (học sinh)

Số học sinh nữ ban đầu là:

54 : (2+1) = 18 (học sinh)

Đáp số: 18 học sinh

Bài 2: Trong một kì thi học sinh giỏi, người ta thấy số học sinh nam bằng $\frac{4}{5}$ số học sinh nữ. Nếu thay 12 bạn học sinh nữ bằng 12 bạn học sinh nam thì số học sinh nữ bằng $\frac{37}{35}$ số học sinh nam. Tính số học sinh nam ban đầu.

Nhận xét: Khi thay 12 bạn nữ bằng 12 bạn nam thì tổng số học sinh vẫn không thay đổi.

Bài giải

Vì tổng số học sinh không thay đổi nên ta chọn tổng số học sinh làm đơn vị.

Ban đầu, số học sinh nam so với tổng số học sinh là: $\frac{4}{4+5}=\frac{4}{9}$ (tổng số học sinh)

Số học sinh nam sau khi tăng thêm 12 bạn so với tổng số học sinh là: $\frac{35}{35+37}=\frac{35}{72}$ (tổng số học sinh)

Phân số chỉ 12 học sinh là:

$\frac{35}{72}-\frac{4}{9}=\frac{1}{24}$ (tổng số học sinh)

Tổng số học sinh tham gia kì thi học sinh giỏi là:

12 x 24 = 288 (học sinh)

Số học sinh nam ban đầu là:

288 : (4+5) x 4 = 128 (học sinh)

Đáp số: 128 học sinh

Bài 3: Một đàn vịt có một số con trên bờ và một số con dưới ao. Lúc đầu số vịt trên bờ bằng $\frac{1}{4}$ số vịt dưới ao. Sau khi có 2 con vịt từ trên bờ nhảy xuống ao thì số vịt trên bờ bằng $\frac{1}{5}$ số vịt dưới ao. Hỏi đàn vịt có bao nhiêu con vịt?

Nhận xét: Do vịt chỉ nhảy từ trên bờ xuống dưới ao nên số lượng đàn vịt không hề thay đổi.

Bài giải

Vì tổng số con vịt không thay đổi nên ta chọn tổng số con vịt làm đơn vị

Lúc đầu, số vịt trên bờ so với tổng số con vịt là: $\frac{1}{1+4}=\frac{1}{5}$ (tổng số con vịt)

Sau khi có 2 con vịt từ trên bờ nhảy xuống thì số vịt trên bờ so với tổng số con vịt là: $\frac{1}{1+5}=\frac{1}{6}$ (tổng số con vịt)

Phân số chỉ 2 con vịt là:

$\frac{1}{5}-\frac{1}{6}=\frac{1}{30}$ (tổng số con vịt)

Tổng số con vịt là:

2 x 30 = 60 (con)

Đáp số: 60 con

2. Hiệu hai số không thay đổi

Trong các bài toán liên quan đến tỉ số, nếu nhắc đến hiệu hai số không thay đổi thì chúng ta có thể nghĩ ngay đến bài toán về tuổi. Hiệu số tuổi của hai người không thay đổi.

a) Ví dụ minh họa: Hiện nay tuổi con bằng $\frac{1}{6}$ tuổi bố. 8 năm nữa, tuổi bố bằng $\frac{22}{7}$ tuổi con. Hỏi hiện nay bố bao nhiêu tuổi, con bao nhiêu tuổi?

Nhận xét: Chúng ta thấy hiệu số tuổi của hai bố con không hề thay đổi.

Bài giải

Vì hiệu số tuổi của bố và con không thay đổi nên ta chọn hiệu số tuổi làm đơn vị.

Hiện nay, tuổi bố so với hiệu số tuổi của bố và con là: $\frac{6}{6-1}=\frac{6}{5}$ (hiệu số tuổi)

8 năm nữa, tuổi bố so với hiệu số tuổi của bố và con là: $\frac{22}{22-7}=\frac{22}{15}$ (hiệu số tuổi)

Phân số chỉ 8 năm là:

$\frac{22}{15}-\frac{6}{5}=\frac{4}{15}$ (hiệu số tuổi)

Bố hơn con số tuổi là:

$8:\frac{4}{15}=30$ (tuổi)

Hiện nay, tuổi của bố là:

30 : (6-1) x 6 = 36 (tuổi)

Hiện nay, tuổi của con là:

36 - 30 = 6 (tuổi)

Đáp số: Bố 36 tuổi

Con 6 tuổi

b) Bài tập

Bài 1: Một thư viện có số sách tham khảo bằng $\frac{4}{7}$ số sách giáo khoa. Nếu thư viện nhập thêm mỗi loại 35 quyển nữa thì số sách tham khảo bằng $\frac{33}{56}$ số sách giáo khoa. Tính số sách giáo khoa ban đầu của thư viện.

Nhận xét: Vì thư viện cùng nhập thêm mỗi loại 35 quyển sách nên hiệu số quyển sách ban đầu giữa hai loại không hề thay đổi.

Bài giải

Vì hiệu số quyển sách không thay đổi nên ta chọn hiệu số quyển sách làm đơn vị.

Ban đầu, số sách giáo khoa so với hiệu số quyển sách là: $\frac{7}{7-4}=\frac{7}{3}$ (hiệu số quyển sách)

Sau khi nhập thêm mỗi loại 35 quyển thì số sách giáo khoa so với hiệu số quyển sách là: $\frac{56}{56-33}=\frac{56}{23}$ (hiệu số quyển sách)

Phân số chỉ 35 quyển sách là:

$\frac{56}{23}-\frac{7}{3}=\frac{7}{69}$ (hiệu số quyển sách)

Sách giáo khoa hơn sách tham khảo số quyển là:

$35:\frac{7}{69}=345$ (quyển)

Số sách giáo khoa ban đầu là:

345 : (7 - 4) x 7 = 805 (quyển)

Đáp số: 805 quyển.

Bài 2: Nhà bác Tân nuôi một đàn gà và vịt. Lúc đầu bác đếm thấy số gà nhiều gấp 2 lần số vịt. Sau đó bác đem mỗi loại 40 con ra chợ bán thì số vịt lúc này lại bằng $\frac{5}{14}$ số gà. Hỏi ban đầu nhà bác Tân có bao nhiêu con cả gà và vịt?

Nhận xét: Vì bác cùng đem mỗi loại 40 con ra chợ bán nên hiệu số con gà và con vịt vẫn không thay đổi.

Bài giải

Vì hiệu số con gà và con vịt không thay đổi nên ta chọn hiệu số con gà và vịt làm đơn vị.

Ban đầu, số con gà so với hiệu số con gà và con vịt là: $\frac{2}{2-1}=\frac{2}{1}$ (hiệu số con gà và con vịt)

Sau khi đem 40 con ra chợ bạn thì số con gà so với hiệu số con gà và con vịt là: $\frac{14}{14-5}=\frac{14}{9}$ (hiệu số con gà và con vịt)

Phân số chỉ 40 con là:

$\frac{2}{1}-\frac{14}{9}=\frac{4}{9}$ (hiệu số con gà và con vịt)

Gà hơn vịt số con là:

$40:\frac{4}{9}=90$ (con)

Học sinh quan sát sơ đồ sau để hiểu rõ hơn:

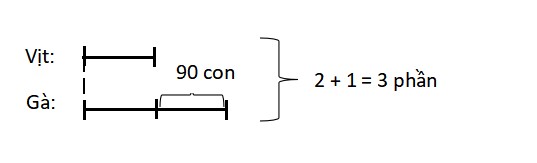
Tổng số con gà và con vịt là:

90 x (2 + 1) = 270 (con)

Đáp số: 270 con

Bài 3: Tìm hai số biết số lớn bằng $\frac{5}{4}$ số bé. Sau khi cùng bớt ở mỗi số đi 7 đơn vị thì số bé bằng $\frac{3}{4}$ số lớn. Tìm hai số lúc đầu.

Nhận xét: Vì cùng bớt ở cả hai số đi 7 đơn vị nên hiệu giữa số lớn và số bé vẫn không thay đổi.

Bài giải

Vì hiệu của hai số không thay đổi nên ta chọn hiệu của hai số làm đơn vị.

Lúc đầu, số lớn so với hiệu của hai số là: $\frac{5}{5-4}=\frac{5}{1}$ (hiệu của hai số)

Sau khi bớt ở số lớn đi 7 đơn vị thì số lớn so với hiệu của hai số là: $\frac{4}{4-3}=\frac{4}{1}$ (hiệu của hai số)

Phân số chỉ 7 đơn vị là:

$\frac{5}{1}-\frac{4}{1}=\frac{1}{1}$ (hiệu của hai số)

Số lớn ban đầu là:

7 x 5 = 35

Số bé ban đầu là:

7 x 4 = 28

Đáp số: 35 và 28

3. Một trong hai đại lượng không thay đổi

a) Ví dụ minh họa: Một lớp học có số học sinh nữ bằng $\frac{2}{3}$ số học sinh nam. Sang học kì 2, có thêm 5 em học sinh nữ chuyển vào, lúc này số học sinh nam bằng $\frac{6}{5}$ số học sinh nữ. Hỏi ban đầu lớp có bao nhiêu học sinh nữ?

Nhận xét: Tổng số học sinh có sự thay đổi (tăng thêm 5 học sinh), Số học sinh nữ thay đổi nên hiệu số học sinh nam và nữ cũng thay đổi. Ở bài toán này, chúng ta chỉ thấy duy nhất số lượng học sinh nam là không thay đổi.

Bài giải

Vì số học sinh nam không thay đổi nên ta chọn số học sinh nam làm đơn vị.

Ban đầu, số học sinh nữ so với số học sinh nam là: $\frac{2}{3}$ (học sinh nam)

Sau khi có thêm 5 học sinh nữ thì số học sinh nữ so với số học sinh nam là: $\frac{5}{6}$ (học sinh nam)

Phân số chỉ 5 học sinh là:

$\frac{5}{6}-\frac{2}{3}=\frac{1}{6}$ (học sinh nam)

Số học sinh nam ban là:

5 x 6 = 30 (học sinh)

Số học sinh nữ ban đầu là:

$30\times\frac{2}{3}=20$ (học sinh)

Đáp số: 20 học sinh

b) Bài tập

Bài 1: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu giảm chiều dài đi 5m thì chiều dài sẽ bằng $\frac{5}{2}$ lần chiều rộng. Hỏi diện tích của hình chữ nhật ban đầu là bao nhiêu?

Bài giải

Vì chiều rộng của hình chữ nhật không thay đổi nên ta chọn chiều rộng làm đơn vị.

Chiều dài ban đầu so với chiều rộng là: $\frac{3}{1}$ (chiều rộng)

Sau khi giảm đi 5m, chiều dài so với chiều rộng là: $\frac{5}{2}$ (chiều rộng)

Phân số chỉ 5m là:

$\frac{3}{1}-\frac{5}{2}=\frac{1}{2}$ (chiều rộng)

Chiều rộng của hình chữ nhật là:

5 x 2 = 10 (m)

Chiều dài ban đầu của hình chữ nhật là:

10 x 3 = 30 (m)

Diện tích của hình chữ nhật ban đầu là:

10 x 30 = 300 ( $m^2$ )

Đáp số: 300 $m^2$

Bài 2: Nhà An có một đàn gà trống và gà mái. Lúc đầu số trống bằng $\frac{2}{5}$ số gà mái. Sau khi đem 10 con gà trống ra chợ bán thì số gà trống bằng $\frac{3}{10}$ số gà mái. Hỏi lúc đầu đàn gà nhà An có bao nhiêu con?

Bài giải

Vì số con gà mái không thay đổi nên ta chọn số gà mái làm đơn vị.

Phân số chỉ 10 con gà là:

$\frac{2}{5}-\frac{3}{10}=\frac{1}{10}$ (số gà mái)

Có số con gà mái là:

10 x 10 = 100 (con)

Số con gà trống lúc đầu là:

$100\times\frac{2}{5}=40$ (con)

Tổng số con gà trống và mái lúc đầu là:

100 + 40 = 140 (con)

Đáp số: 140 con

Bài 3: Một cửa hàng bán hai loại áo: áo sơ mi và áo cộc tay. Buổi sáng, chủ cửa hàng đếm thấy số lượng áo sơ mi nhiều gấp 4 lần áo cộc tay. Buổi chiều, sau khi bán được 16 chiếc áo sơ mi thì số lượng áo cộc tay bằng $\frac{1}{2}$ số lượng áo sơ mi. Hỏi ban đầu cửa hàng có bao nhiêu chiếc áo sơ mi?

Bài giải

Vì số lượng áo cộc tay không thay đổi nên ta chọn số lượng áo cộc tay làm đơn vị.

Ban đầu, số lượng áo sơ mi so với áo cộc tay là: $\frac{4}{1}$ (áo cộc tay)

Sau khi bán được 16 cái áo sơ mi, số lượng áo sơ mi so với áo cộc tay là: $\frac{2}{1}$ (áo cộc tay)

Phân số chỉ 16 cái áo là:

$\frac{4}{1} - \frac{2}{1}=\frac{2}{1}$ (áo cộc tay)

Ban đầu cửa hàng có số áo cộc tay là:

16 : 2 x 1 = 8 (chiếc áo)

Ban đầu cửa hàng có số áo sơ mi là:

8 x 4 = 32 (chiếc áo)

Đáp số: 32 chiếc áo

>>Bài tiếp theo: Bài Toán Tỉ Lệ Thuận, Tỉ Lệ Nghịch Toán 5

Bài Toán Tỉ Lệ Thuận, Tỉ Lệ Nghịch Toán 5 được GiaiToan chia sẻ trên đây. Với bài tập cụ thể kèm theo lời giải sẽ là tài liệu hữu ích cho các em tham khảo, dựa vào đó để rèn luyện kỹ năng giải bài tập Toán lớp 5: Ôn tập giải toán. Chúc các em học tốt, ngoài việc tham khảo tài liệu trên các em cũng có thể tham khảo thêm Lý thuyết Toán lớp 5, Giải Toán Lớp 5, Luyện Tập Toán Lớp 5, Vở Bài Tập Toán Lớp 5 được GiaiToan biên soạn nhé