Giaitoan.com Toán 10

Đường trung tuyến là gì? Công thức tính độ dài đường trung tuyến

Nội dung
  • 5 Đánh giá

Đường trung tuyến

GiaiToan.com xin giới thiệu tới quý thầy cô và các bạn học sinh tài liệu tham khảo Định nghĩa đường trung tuyến. Bộ tài liệu gồm câu hỏi bài tập các dạng bài thường gặp trong các kì thi, kiểm tra trong chương trình Toán lớp 10. Tài liệu được GiaiToan biên soạn và đăng tải, hi vọng sẽ giúp các bạn ôn tập kiến thức môn Toán hiệu quả, sẵn sàng cho những kì thi sắp tới. Mời thầy cô và học sinh cùng tham khảo!

A. Trung tuyến là gì?

- Đường trung tuyến của tam giác là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện của tam giác đó.

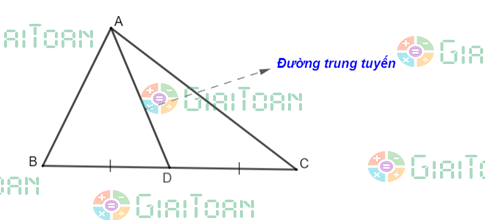
Đường trung tuyến là gì

- Mỗi tam giác có 3 đường trung tuyến.

Cách vẽ đường trung tuyến

Bước 1: Vẽ tam giác ABC.

Bước 2: Vẽ trung điểm của đoạn thẳng BC, đặt tên điểm này là D.

Bước 3: Vẽ trung điểm của đoạn thẳng AB, đặt tên điểm này là E.

Bước 4: Vẽ trung điểm của đoạn thẳng AC, đặt tên điểm này là F.

Bước 5: Vẽ trung tuyến AD.

Bước 6: Vẽ trung tuyến BE.

Bước 7: Vẽ trung tuyến CF.

Bước 8: Vẽ giao điểm của AD; BE và CF, đặt tên giao điểm này là G.

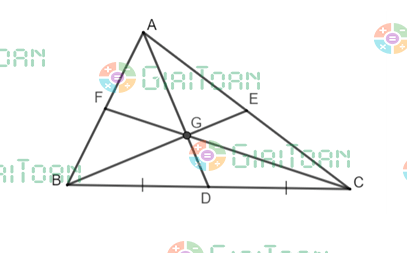
Đường trung tuyến là gì

B. Tính chất đường trung tuyến

Tính chất 1: Ba đường trung tuyến của tam giác đồng quy tại một điểm được gọi là trọng tâm.

Ta có 3 đường trung tuyến AD, BE, FC giao nhau tại G => G là trọng tâm tam giác

Tính chất 2: Khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng \frac{2}{3} đường trung tuyến tương ứng với đỉnh đó.

=> \frac{{AG}}{{AD}} = \frac{{BG}}{{BE}} = \frac{{CG}}{{CF}} = \frac{2}{3} (1)

Tính chất 3: Khoảng cách từ trọng tâm đến trung điểm mỗi cạnh bằng \frac{1}{3} đường trung tuyến tương ứng với điểm đó.

=> \frac{{GD}}{{AD}} = \frac{{GE}}{{BE}} = \frac{{GF}}{{CF}} = \frac{1}{3} (2)

Từ (1) và (2) => \frac{{BG}}{{GE}} = \frac{{AG}}{{GD}} = \frac{{CG}}{{GF}} = 2

C. Đường trung tuyến trong tam giác vuông

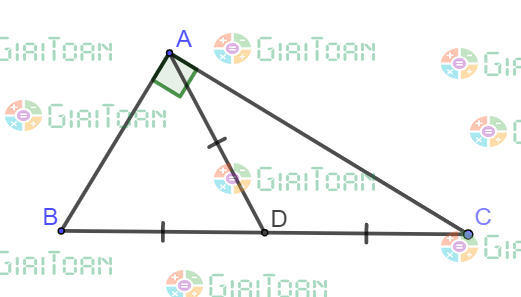
Đường trung tuyến là gì

- Đường trung tuyến của tam giác vuông sẽ có đầy đủ những tính chất của một đường trung tuyến tam giác.

Định lý 1: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

=> AD = BC/2

=> AD = BD = DC

Định lý 2: Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

D. Đường trung tuyến trong tam giác cân

- Định lý: Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy vừa là đường cao, đường trung trực và đường phân giác.

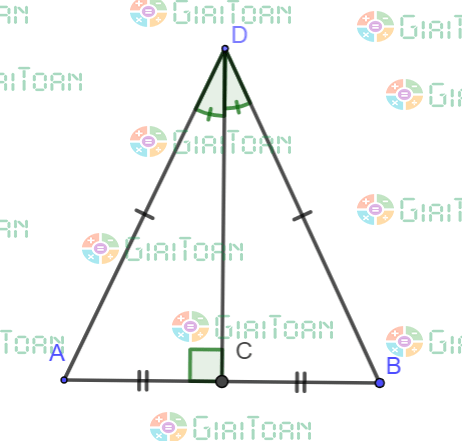
Đường trung tuyến là gì

E. Công thức tính độ dài đường trung tuyến

- Cho tam giác ABC có độ dài các cạnh AB = c; AC = b; BC = a, các đường trung tuyến {m_a},{m_b},{m_c}

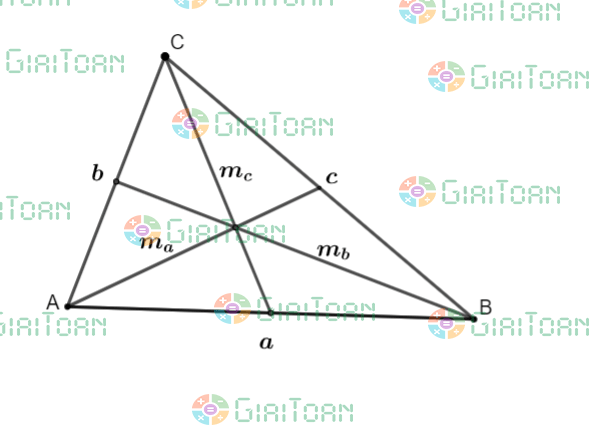
Đường trung tuyến là gì

Ta có công thức tính độ dài đường trung tuyến như sau:

\begin{array}{*{20}{c}} {{m_a}^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}{\text{ }}} \\ {{m_b}^2 = \dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4}} \\ {{m_c}^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}{\text{ }}} \end{array}

Phát biểu công thức:

Công thức tính độ dài đường trung tuyến của cạnh bất kỳ bằng căn bậc 2 của một phần hai tổng bình phương hai cạnh kề trừ một phần tư bình phương cạnh đối.

F. Bài tập về tính chất ba đường trung tuyến

Bài 1: Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH như hình vẽ

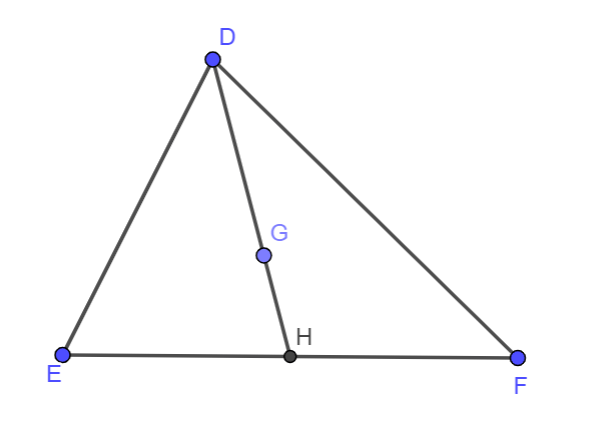
Đường trung tuyến là gì?

Trong các khẳng định sau đây, khẳng định nào đúng?

\frac{{DG}}{{GH}} = 3

\frac{{GH}}{{DH}} = \frac{1}{3}
\frac{{DG}}{{DH}} = \frac{1}{2}\frac{{GH}}{{DG}} = \frac{2}{3}

Bài 2: Cho hình vẽ dưới đây:

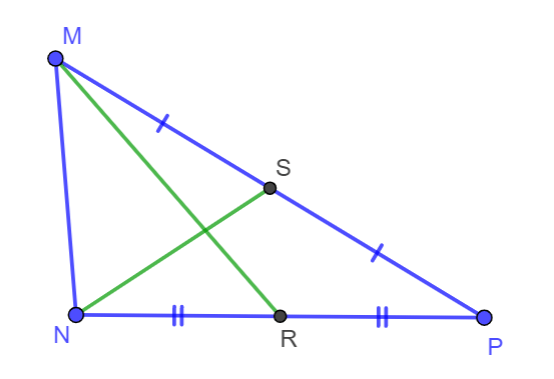
Đường trung tuyến là gì?

Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a. MG = … MR ; GR = … MR ; GR = … MG

b. NS = … NG ; NS = … GS ; NG = … GS.

Bài 3: Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:

Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.

Bài 4: Chứng minh định: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Bài 5: Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Bài 6: Cho tam giác DEF cân tại D với đường trung tuyến DI.

a) Chứng minh ΔDEI = ΔDFI.

b) Các góc DIE và góc DIF là những góc gì?

c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.

Bài 7: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng: GA = GB = GC.

Bài 8: Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.

a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.

b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.

------------------------------------------------------------

Hy vọng tài liệu sẽ giúp các bạn tiếp xúc với nhiều dạng bài về Công thức đường trung tuyến. Đây cũng là phần kiến thức thường xuất hiện trong các bài thi, bài kiểm tra môn Toán lớp 7, chính vì vậy việc nắm vững các kiến thức về tam giác là rất quan trọng giúp các em học sinh có thể đạt điểm cao trong các bài thi của mình. Hy vọng tài liệu trên sẽ giúp các em học sinh ghi nhớ lý thuyết về tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng hơn. Chúc các em học tốt.

Chia sẻ bởi: Người Nhện
Mời bạn đánh giá!
  • Lượt xem: 385
Tìm thêm: công thức toán 10 Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần