Giaitoan.com Toán 9 Chuyên đề Toán 9 thi vào 10

Đề thi thử vào 10 môn Toán năm học 2021 - 2022 sở GD & ĐT Tỉnh Vĩnh Long Đề thi vào 10 môn Toán có đáp án

Nội dung
  • 2 Đánh giá

Đề thi thử môn Toán 2021

Đề thi thử môn Toán vào 10 năm học 2021 - 2022 sở GD&ĐT Tỉnh Vĩnh Long được giaitoan.com biên tập bao gồm đề và hướng dẫn đáp án chi tiết giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết các câu hỏi từ cơ bản đến nâng cao Toán lớp 9. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong kì thi tuyển sinh vào lớp 10 môn Toán. Mời các bạn cùng tham khảo chi tiết. Chúc các em học sinh ôn tập thật tốt!

Đề thi tuyển sinh vào lớp 10 môn Toán

SỞ GIÁO DỤC VÀ ĐÀO TẠO

TỈNH VĨNH LONG

---------------------------

ĐỀ THI CHÍNH THỨC

(Đề thi gồm có 01 trang)

KỲ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN

NĂM HỌC: 2021 - 2022

MÔN THI: TOÁN

Thời gian: 150 phút (không kể thời gian phát đề)

--------------------------------------------------------------------------------------------------------

Câu 1. (2,0 điểm)

a) Cho biểu thức A = \frac{x}{{\sqrt x - 1}} và B = \frac{{x\sqrt x - 1}}{{\sqrt x + 1}} - 1 với x > 0,x \ne 1. Rút gọn A và chứng minh B > A.

b) So sánh \sqrt {24} + \sqrt {26} và 10.

Câu 2. (1,0 điểm) Cho Parabol \left( P \right):y = {x^2} và đường thẳng (d): y = \left( {m - 1} \right)x + m + 4 (m là tham số). Tìm m để (d) cắt (P) tại 2 điểm nằm về 2 phía của trục tung.

Câu 3. (1,5 điểm)

a) Giải phương trình: \sqrt {43 - x} = x - 1

b) Giải hệ phương trình: \left\{ {\begin{array}{*{20}{c}} {x + \dfrac{x}{{x - y}} = \dfrac{{ - 1}}{2}} \\ {2y - \dfrac{y}{{x - y}} = \dfrac{3}{2}} \end{array}} \right.

Câu 4. (1,5 điểm)

a) Chứng minh rằng tổng các bình phương của 6 số nguyên liên tiếp không thể là số chính phương.

b) Tìm các nghiệm nguyên dương của phương trình: {x^2}y + 2xy + y = 32x

Câu 5. (1,0 điểm) Cho hình vuông ABCD và điểm E trên cạnh BC biết AB = 4cm, BE = \frac{3}{4}BC. Tia Ax vuông góc với AE tại A cắt tia CD tại F.

a) Tính diện tích \Delta AEF

b) Gọi I là trung điểm của đoạn thẳng EF, tia AI cắt CD tại K. Chứng minh: A{E^2} = FK.CF

Câu 6. (2,0 điểm) Cho và điểm M sao cho OM = 2R. Kẻ các tiếp tuyến MA, MB với (A, B là các tiếp điểm). Trên đoạn thẳng AB lấy điểm I (Với AI < BI và I khác A). Qua I vẽ dây CD sao cho IC = ID và C thuộc cung nhỏ AB. Tiếp tuyến của tại C cắt OI tại Q. Chứng minh:

a) Tứ giác OCQD nội tiếp được đường tròn.

b) \Delta AMB là tam giác đều

c) OQ \bot MQ

Câu 7. (1,0 điểm) Cho số thực x thỏa mãn 1 \leqslant x \leqslant 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: T = \frac{{3 + x}}{x} + \frac{{6 - x}}{{3 - x}}

-------------------------------------------------- HẾT ------------------------------------------

Thí sinh được sử dụng các loại máy tính cầm tay do Bộ Giáo dục và Đào tạo cho phép.

Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không được giải thích gì thêm.

Họ và tên thí sinh:....................................... Số báo danh:………………………

Đáp án đề thi tuyển sinh lớp 10 môn Toán

(Còn tiếp)

------------------------------------------------------

Trên đây giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi vào lớp 10 môn Toán Sở GD&ĐT tỉnh Vĩnh Long. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập liên quan: Đề Thi Giữa Kì 2 Lớp 9, Đề Thi Học Kì 2 Lớp 9, Chuyên đề Toán 9 luyện thi vào 10, .....

SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH VĨNH LONG
---------------------------
ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN
KỲ THI TUYỂN SINH LỚP 10 CHUYÊN
Năm học: 2021 - 2022
MÔN THI: TOÁN
Thời gian làm bài: 120 phút
(Không kể thời gian phát đề)
-------------------------------------------------------------------------------------------
Câu 1. (2,0 điểm)
a) Cho biểu thức
2
1
−
=−
−−
x x x
A
x x x
và
1
1
1
+
=−
+
xx
B
x
với
0, 1.xx
Rút gọn A và chứng
minh B > A.
b) So sánh
24 26+
và 10.
Câu 2. (1,0 điểm)
Cho Parabol (P):
2
=yx
và đường thẳng (d):
(m là tham số). Tìm m
để (d) cắt (P) tại 2 điểm nằm về 2 phía của trục tung.
Câu 3. (1,5 điểm)
a) Giải phương trình:
43 1− = −xx
b) Giải hệ phương trình:
1
2
3
2
2
−
+=
−
−=
−
x
x
xy
y
y
xy
Câu 4. (1,5 điểm)
a) Chứng minh rằng tổng các bình phương của 6 số nguyên liên tiếp không thể là số chính
phương.
b) Tìm các nghiệm nguyên dương của phương trình:
2
2 32+ + =x y xy y x
Câu 5. (1,0 điểm) Cho hình vuông ABCD và điểm E trên cạnh BC biết AB = 4cm,
3
4
=BE BC
.
Tia Ax vuông góc với AE tại A cắt tia CD tại F.
a) Tính diện tích
AEF
b) Gọi I là trung điểm của đoạn thẳng EF, tia AI cắt CD tại K. Chứng minh:
2
.=AE KF CF
Câu 6. (2,0 điểm)
Cho
( )
;OR
và điểm M sao cho OM = 2R. Kẻ các tiếp tuyến MA, MB với
( )
O
(A, B là
các tiếp điểm). Trên đoạn thẳng AB lấy điểm I (Với AI < BI và I khác A). Qua I vẽ dây CD
sao cho IC = ID và C thuộc cung nhỏ AB. Tiếp tuyến của
( )
O
tại C cắt OI tại Q. Chứng
minh:
a) Tứ giác OCQD nội tiếp được đường tròn.
b)
AMB
là tam giác đều
c)
OQ MQ⊥
Câu 7. (1,0 điểm) Cho số thực x thỏa mãn
12x
. Tìm giá trị lớn nhất và giá trị nhỏ nhất
của biểu thức:
36
3
+−
=+
−
xx
T
xx
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =
HƯỚNG DẪN ĐÁP ÁN ĐỀ CHÍNH THỨC MÔN TOÁN
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN
NĂM HỌC 2021 - 2022
---------------------------------------------------------------
Câu 1. (2,0 điểm)
Với
0, 1.xx
Ta có:
( )
( )
21
2
11
1
−
−
= − = −
− − −
−
xx
x x x x
A
x x x x
xx
2 1 2 1
1
1 1 1
− − +
= − = = −
− − −
x x x x
x
x x x
( )( )
( )
11
1
1 1 1 1
11
+ − +
+
= − = − = − + − = −
++
x x x
xx
B x x x x
xx
Ta lại có:
( ) ( )
2
1 2 1 1 0− = − − − = − + = − B A x x x x x x
với
0, 1.xx
BA
(đpcm)
b) Ta có:
( )
2
2
24 26 24 26 2. 24.26 50 2. 624 50 2. 625 100 10+ = + + = + + = =
24 26 10 +
Câu 2. (1,0 điểm)
Xét PT hoành độ giao điểm:
( ) ( ) ( )
22
1 4 1 4 0 *= − + + − − − − =x m x m x m x m
Ta có:
( ) ( )
( )
( )
22
22
1 4 4 2 1 4 16 2 1 16 1 16 0= − − − − = − + + + = + + + = + + m m m m m m m m m
pt (*) luôn có 2 nghiệm phân biệt hay (d) luôn cắt (P) tại 2 điểm phân biệt
m
Theo Vi-et ta có:
12
12
1
4
+ = −
= − −
x x m
x x m
Để (d) cắt (P) tại 2 điểm nằm về 2 phía của trục tung thì pt (*) luôn có 2 nghiệm phân biệt
trái dấu hay:
4 0 4− − −mm
Câu 3. (1,5 điểm)
a) ĐK:
43 0 43− xx
Phương trình
( )
( )( )
2
22
10
1 1 43
1 43
7
7 6 0
43 2 1 42 0
43 1
−


=
− + =
− = − + − − =
− = −


x
xx
x
x
xx
x x x x x
xx
b) ĐK:
xy
Hệ phương trình
( ) ( ) ( )
( ) ( ) ( )
2
21
2 2 1 1
2
4 2 3 2
43
+ = −
− + = − −
−



− − = −
−=
−
x
x
x x y x x y
xy
y
y x y y x y
y
xy
Cộng vế với vế của (1) với (2) ta được:
( ) ( ) ( )
2 2 4 2 2− + + − − = −x x y x y x y y x y
( )( )
( )
( )
0
2 2 0
20
2
=
−=
− + =
+=
=−
x y KTM
xy
x y x y
xy
x y TM
Với
2=−xy
2 1 7 7
2
3 2 12 6
− − −
− + = = =
−
y
y y x
y
Thử lại ta thấy
( )
7
6
7
12
−
=
=
x
TM
y
Vậy hệ pt có nghiệm là:
7
6
7
12
−
=
=
x
y
Câu 4. (1,5 điểm)
a) Giả sử 6 số nguyên liên tiếp lần lượt là:
( )
; 1; 2; 3; 4; 5+ + + + + x x x x x x x
Ta có:
( ) ( ) ( ) ( ) ( )
2 2 2 2 2
2
1 2 3 4 5+ + + + + + + + + +x x x x x x
2 2 2 2 2 2
2 1 4 4 6 9 8 16 10 25= + + + + + + + + + + + + + + +x x x x x x x x x x x
2 2 2 2 2 2
2
2 1 4 4 6 9 8 16 10 25
6 30 55
= + + + + + + + + + + + + + + +
= + +
x x x x x x x x x x x
xx
b) Ta có:
( )
( )
22
2
32
2 32 2 1 32
1
+ + = + + = =
+
x
x y xy y x y x x x y
x
Do:
( ) ( ) ( ) ( ) ( )
2 2 2 2
2
; 32 1 32 2 1 32 64 32 32 1 32 1
+
+ + + + + − + +x y x x x x x x x x x
( ) ( ) ( )
22
1 32 1;2;4;8;16;32 1 4;16 + = + x U x
(Vì:
( )
2
11+x
và là số chính phương)
TH1:
( )
( )
( )
( )
2
2
1
1 4 2 3 0 8
3
=
+ = + − = =
=−
x TM
x x x y TM
x KTM
TH2:
( )
( )
( )
( )
2
2
3
1 16 2 15 0 6
5
=
+ = + − = =
=−
x TM
x x x y TM
x KTM
Vậy nghiệm của pt là:
( ) ( ) ( )
; 1;8 ; 3;6=xy
Câu 5. (1,0 điểm)
a) Ta có:
13
=AA
(cùng phụ với
2
A
)
Xét
ABE
và
ADF
có:
( )
( )
( )
13
..
90
=
=
==
cmt
ABE ADF g
A
BD
cg
gt
A
AD AE=
(2 cạnh tương ứng)
⊥AEF
cân tại A.
Mà:
3
4
=BE BC
(gt)
( )
3
43
4
= =BE cm
Theo Pi-Ta-Go ta có:
( )
( )
2 2 2 2 2
. 5.5
4 3 5 12,5
22
= + = + = = = =
AEF
AE AF
AE AB BE cm S cm
b) Vì:
⊥AEF
cân tại A (cmt)
11
45 = =EF
Mà:
( )
=FI EI gt AI
là trung trực của EF
; ⊥ AI EF IAE IAF
cân tại I.
= =FI EI AI
Xét
IKF
và
CEF
có:
( )
90
. . .
==
= =
IF KF
IKF CEF g g KF CF IF EF
CF EF
chun
I
F g
C
∽
( )
2 2 2 2
. . . 2 2 = = = = + =KF CF IF EF IF IE IE IE IA AE
(đpcm)
Câu 6. (2,0 điểm)
Chia sẻ bởi: Captain
Mời bạn đánh giá!
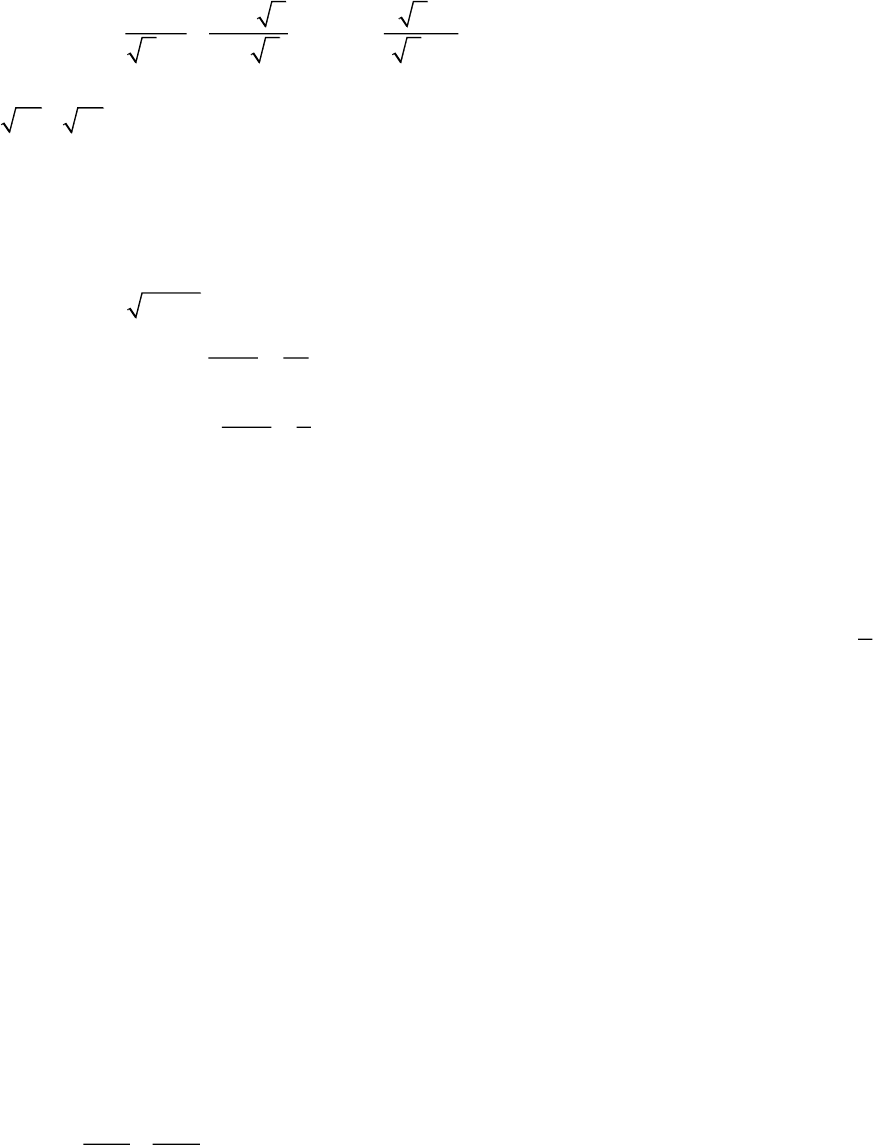
  • Lượt xem: 865
  • Dung lượng: 343,1 KB
Tìm thêm: Đề thi thử vào 10 môn Toán

Mới nhất trong tuần