Giaitoan.com Toán 9 Chuyên đề Toán 9 thi vào 10

Chứng minh các điểm cùng nằm trên đường tròn Đường tròn

Nội dung
  • 1 Đánh giá

Chứng minh 4 điểm cùng nằm trên một đường tròn

Chứng minh nhiều điểm thuộc cùng một đường tròn là một dạng toán khó thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo!

1. Đường tròn là gì?

- Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách đều O một khoảng R kí hiệu là (O; R) hay (O)

+ Đường tròn đi qua các điểm A1, A2, …, An gọi là đường tròn ngoại tiếp đa giác A1A2…An

+ Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác đó.

2. Tính chất của tam giác 

+ Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp tam giác đó

+ Trong tam giác đều, tâm đường tròn ngoại tiếp là trọng tâm của tam giác

+ Trong tam giác thường:

* Tâm đường tròn ngoại tiếp là giao ba đường trung trực của 3 cạnh tam giác đó

* Tâm đường tròn nội tiếp là giao 3 đường phân giác trong của tam giác

3. Cách chứng minh nhiều điểm cùng thuộc đường tròn

Để chứng minh các điểm A1, A2, …, An cùng thuộc một đường tròn ta chứng minh các điểm A1, A2, …, An cách đều điểm O cho trước.

4. Bài tập chứng minh nhiều điểm cùng nằm trên một đường tròn

Ví dụ 1: Cho tam giác ABC cạnh bằng a. Các đoạn thẳng AM, BN, CP lần lượt là các đường trung tuyến. Chứng minh 4 điểm B, P, N, C cùng thuộc một đường tròn. Tính bán kính đường tròn đó.

Hướng dẫn giải

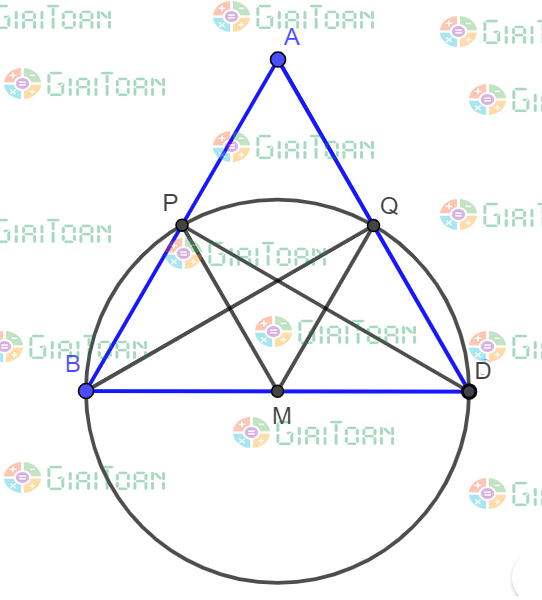
Chứng minh các điểm cùng nằm trên đường tròn

Vì tam giác ABC đều nên cấc trung tuyến đồng thời là đường cao

=> AM, BN, CP lần lượt vuông góc với BC, AC, AB

=> Tam giác BCP, BCN là tam giác vuông

Với BC là cạnh huyền

=> MP = MN = MB = MC

Hay các điểm B, P, N, C cùng thuộc đường tròn

Đường kính BC = a, tâm đường tròn là trung điểm của BC

Ví dụ 2: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi M là trung điểm của AC, G là trọng tâm của tam giác ABM. Gọi Q là giao điểm của BM và GO. Xác định tâm đường tròn ngoại tiếp tam giác BGQ

Hướng dẫn giải

Vì tam giác ABC cân tại A nên tâm O của đường tròn ngoại tiếp tam giác nằm trên đường trung trực của BC.

Gọi K là giao điểm của AO và BM

Dựng các đường trung tuyến MN và BP của tam giác ABM cắt nhau tại trọng tâm G

Do MN // BC

=> MN ⊥ AO

Do K là giao của AO và NM

=> K là trọng tâm tam giác ABC

=> GK // AC

Mặt khác ta có OM ⊥ AC

=> GK ⊥ OM

=> K là trực tâm của tam giác OMG

=> MK ⊥ OG

Như vậy tam giác BGQ vuông tại Q

=> Tâm đường tròn ngoại tiếp tam giác GBQ là trung điểm I của BG

Ví dụ 3: Cho hình vuông ABCD. Gọi M là trung điểm của BC, N là điểm thuộc đường chéo CA sao cho AN = AC/4. Chứng minh 4 điểm M, N, C, D nằm trên cùng một đường tròn.

Hướng dẫn giải

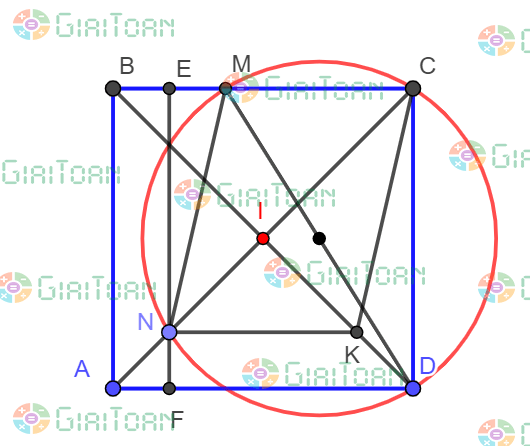
Chứng minh các điểm cùng nằm trên đường tròn

Ta có tứ giác MNCD có góc MCD = 900

=> Để chứng minh 4 điểm M, N, C, D cùng nằm trên một đường tròn ta sẽ chứng minh góc MND = 900

Cách 1: Qua N kẻ đường thẳng song song với AB cắt BC và AD lần lượt tại E và F

Xét hai tam giác vuông NEM và DFN cps

EM = NF = AB/4

EN = DF = AB /4

=> ∆NEM = ∆DFN

\Rightarrow \widehat {NME} = \widehat {DFN},\widehat {MNE} = \widehat {NDF} \Rightarrow \widehat {MNE} + \widehat {DNF} = {90^0}

Hay tam giác MND vuông tại N

=> 4 điểm M, N, C, D cùng nằm trên đường tròn đường kinh MD

Cách 2: Gọi K là trung điểm của DI với I là giao điểm của hai đường chéo

Dễ thấy MCKN là hình bình hành

=> MN // CK

Mặt khác do NK ⊥ CD, DK ⊥ CN => K là trực tâm của tam giác CDN

=> CK ⊥ ND => MN ⊥ ND

5. Bài tập vận dụng chứng minh nhiều điểm cùng nằm trên đường tròn

Bài 1: Cho tam giác BAC nội tiếp đường tròn (O), đường kính AD. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của điểm D lên HB, HC, BC. Chứng minh 4 điểm X, Y, Z, M cùng thuộc một đường tròn.

Bài 2: Cho tam giác ABC trực tâm H. Lấy điểm M, N thuộc tia BC sao cho MN = BC và M nằm giữa B và C. Gọi D, E lần lượt là hình chiếu vuông góc của M, N lên AC, AB. Chứng minh các điểm A, D, E, H cùng thuộc một đường tròn.

------------------------------------------------

Hy vọng tài liệu Chứng minh 4 điểm thuộc cùng một đường tròn sẽ giúp ích cho các bạn học sinh học nắm chắc kiến thức về tương giao đồ thị, hàm số bậc hai đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Ngoài ra mời quý thầy cô và học sinh tham khảo thêm một số nội dung:

Chia sẻ bởi: Mỡ
Mời bạn đánh giá!
  • Lượt xem: 2.020
Tìm thêm: Toán 9 Chuyên đề Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần