Giaitoan.com Toán 10 Toán 11 Toán 12

Dãy số Fibonacci Tìm hiểu về dãy Fibonacci

Nội dung
  • 3 Đánh giá

Giới thiệu về dãy số Fibonacci

Tài liệu về dãy Fibonacci được GiaiToan biên soạn giúp các bạn học sinh hiểu sâu về dãy số này, cũng như cách tính dãy số Fibonacci, công thức tính tổng dãy số Fibonacci, .... Qua đó giúp các bạn học sinh tăng thêm niềm yêu thích với Toán học. Mời các bạn học sinh tham khảo tài liệu.

1. Dãy số Fibonacci là gì?

Dãy số Fibonacci là một dãy số vô hạn, bắt đầu bởi số 0 và 1, các số tiếp theo bằng tổng của hai số liền trước.

Như vậy ta sẽ có dãy số Fibonacci là: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ….

Bài toán nuôi thỏ

Dãy Fibonacci bắt nguồn từ bài toán về việc sinh sản của các cặp thỏ. Bắt đầu với một thỏ đực và một thỏ cái, trong điều kiện lý tưởng hỏi có bao nhiêu cặp thỏ có thể được sinh ra trong một năm?

Bài toán được giải theo sơ đồ sau:

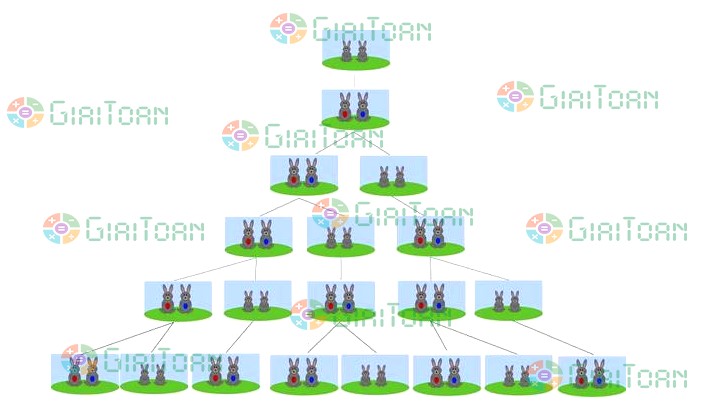
Dãy số Fibonacci

Sau một tháng, cặp thỏ ban đầu chưa thuần thục sinh dục và không thể giao phối.

Sau hai tháng, cặp thỏ đã giao phối nhưng chưa sinh thỏ con, nên ta chỉ có một cặp thỏ.

Sau ba tháng, cặp thỏ ban đầu sinh ra một cặp thỏ con, kết quả là có hai cặp thỏ.

Hết tháng thứ tư thì cặp thỏ ban đầu lại sinh thỏ con, và cặp thỏ thứ hai thì giao phối nhưng chưa sinh thỏ con, ta có tổng cộng ba cặp thỏ.

Cứ tiếp tục như thế cho đến hết năm ta sẽ có 233 cặp thỏ.

2. Công thức tổng quát của dãy số Fibonacci

Công thức truy hồi của dãy Fibonacci

{F_n} = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n = 1 \hfill \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n = 2 \hfill \\ F\left( {n - 1} \right) + F\left( {n - 2} \right),\,\,\,\,\,\,n > 2 \hfill \\ \end{gathered} \right.\,

Công thức tổng quát cho dãy số Fibonacci

{F_n} = \frac{1}{{\sqrt 5 }}\left[ {{{\left( {\frac{{1 + \sqrt 5 }}{2}} \right)}^n} - {{\left( {\frac{{1 - \sqrt 5 }}{2}} \right)}^n}} \right]

Ví dụ:

Với n = 3 ta có:

\begin{matrix} {F_3} = \dfrac{1}{{\sqrt 5 }}\left[ {{{\left( {\dfrac{{1 + \sqrt 5 }}{2}} \right)}^3} - {{\left( {\dfrac{{1 - \sqrt 5 }}{2}} \right)}^3}} \right] \hfill \\ = \dfrac{1}{{\sqrt 5 }}\left[ {\dfrac{{1 + 3\sqrt 5 + 3.5 + 5\sqrt 5 }}{8} - \dfrac{{1 - 3\sqrt 5 + 3.5 - 5\sqrt 5 }}{8}} \right] \hfill \\ = \dfrac{1}{{\sqrt 5 }}.\dfrac{{6\sqrt 5 + 10\sqrt 5 }}{8} = \dfrac{1}{{\sqrt 5 }}.\dfrac{{16\sqrt 5 }}{8} = 2 \hfill \\ \end{matrix}

Công thức tính tổng dãy số Fibonacci

Công thức tính tổng số n số Fibonacci với mọi số n ≥ 2 như sau:

\sum\limits_{i = 1}^n {{F_i} = {F_{n + 2}} - 1}

Số thứ 100 trong dãy số Fibonacci là số mấy?

Áp dụng công thức tổng quát của dãy số Fibonacci, số thứ 100 (n = 100) trong dãy số là:

{F_{100}} = \frac{1}{{\sqrt 5 }}\left[ {{{\left( {\frac{{1 + \sqrt 5 }}{2}} \right)}^{100}} - {{\left( {\frac{{1 - \sqrt 5 }}{2}} \right)}^{100}}} \right] = 3,{542248482.10^{20}}

-------

Trên đây, GiaiToan đã giới thiệu một số kiến thức cơ bản về dãy Fibonacci, ngoài ra các bạn học sinh có thể tham khảo thêm các tài liệu về Toán học được GiaiToan đăng tải. Với những tài liệu này sẽ giúp các bạn học tập tốt hơn ở môn Toán.

Chia sẻ bởi: Thùy Chi
Mời bạn đánh giá!
  • Lượt xem: 4.229
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần