Giaitoan.com Toán 8 Luyện tập Toán 8

Chứng minh hình vuông Luyện tập Toán 8

Nội dung
  • 1 Đánh giá

Hình vuông

Chuyên đề Toán 8: Chứng minh hình vuông đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh lớp 8 ôn tập và củng cố kiến thức về dạng toán về tứ giác. Tài liệu bao gồm công thức, các dạng toán, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề tứ giác Toán lớp 8. Chúc các bạn học tập hiệu quả!

1. Dấu hiệu nhận biết hình vuông

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông

- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông

- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông

- Hình thoi có một góc vuông là hình vuông

- Hình thoi có hai đường chéo bằng nhau là hình vuông

2. Bài tập chứng minh hình vuông

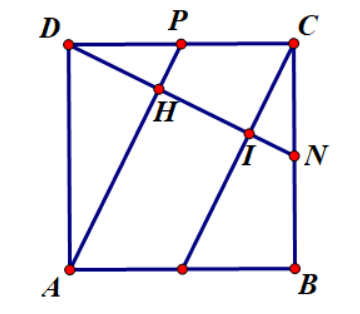
Ví dụ 1: Cho hình vuông ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Đoạn thẳng CP cắt DQ tại I

a) Chứng minh rằng CP = DQ và CP \bot DQ

b) Vẽ  AH \bot DQ tại H, AH cắt CD tại M. Chứng minh rằng M là trung điểm của CD

c) Chứng minh rằng AI = AB

Hướng dẫn giải:


a) Xét \Delta CMB và \Delta DNC có:

CD = BC ( ABCD là hình vuông)

( ABCD là hình vuông)

\widehat {DCN} = \widehat {CBM} = {90^ \circ }

CN = MB (P, N là trung điểm của CD, BC )

\Delta CMB = \Delta DNC\left( {c.g.c} \right) \Rightarrow CM = DN;\,\,\widehat {\,MCB} = \widehat {NDC}

Mặt khác \,\widehat {\,CND} + \widehat {CDN} = {90^ \circ } \Rightarrow \widehat {BCM} + \widehat {CND} = {90^ \circ } \Rightarrow CM \bot DN

b) Ta có: \left\{ \begin{array}{l} AP \bot DN\\ CM \bot DN \end{array} \right. \Rightarrow AP//CM \Rightarrow \widehat {APD} = \widehat {DCM}( đồng vị)

\Rightarrow \widehat {DAP} = \widehat {BCM}( cùng phụ với \widehat {APD} )

Xét  \Delta ADP và \Delta CBM  có:

\widehat {PDA} = \widehat {CBM} = {90^ \circ }

AD = CB ( ABCD là hình vuông )

\widehat {DAP} = \widehat {BCM}( cmt)

\Delta ADP = \Delta CBM\left( {g.c.g} \right) \Rightarrow DP = BM = \dfrac{{AB}}{2}

Vì P \in CD mà AB = CD và  DP = \dfrac{{AB}}{2} \Rightarrow PD = PC. Vậy P là trung điểm của CD

c) Xét \Delta CDI có PH // CI và P là trung điểm của CD \Rightarrow H là trung điểm của của DI

Trong  \Delta ADI có AH là đường cao đồng thời là đường trung tuyến \Rightarrow \Delta ADIcân tại A. Vậy AI = AD = AB

Ví dụ 2: Cho tứ giác ABCD có \widehat {ADC} + \widehat {BCD} = {90^ \circ } và AD = BC. Gọi M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD. Chứng minh rằng MNPQ là hình vuông

Hướng dẫn giải

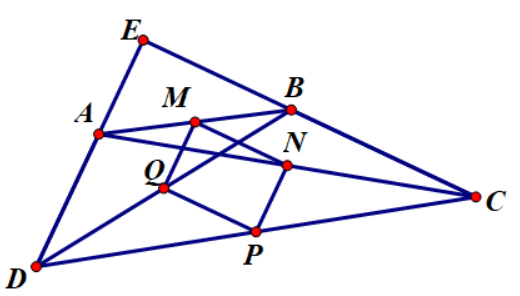
Gọi E là giao điểm của AD và BC

Ta có:\widehat {ADC} + \widehat {BCD} = {90^ \circ } \Rightarrow \widehat {DEC} = {90^ \circ } \Rightarrow AD \bot BC

Xét tam giác ABC có

M là trung điểm của AB

N là trung điểm của AC

MN là đường trung bình của \Delta ABC \Rightarrow \left\{ \begin{array}{l} MN//BC\\ MN = \dfrac{1}{2}BC \end{array} \right.

Tương tự ta chứng minh được

QP là đường trung bình của tam giác \Delta BCD \Rightarrow \left\{ \begin{array}{l} QP//BC\\ QP = \dfrac{1}{2}BC \end{array} \right.

QM là đường trung bình của tam giác \Delta ACD \Rightarrow \left\{ \begin{array}{l} PN//AD\\ PN = \dfrac{1}{2}AD \end{array} \right.

Mà AD = BC \Rightarrow MN = QP = MQ = PN(1)

Ta có:\left\{ \begin{array}{l} MN//BC\\ QM//AD\\ BC \bot AD \end{array} \right. \Rightarrow QM \bot MN \Rightarrow \widehat {QMN} = {90^ \circ }\,\,\,\,\left( 2 \right)

Từ (1) và (2) suy ra MNPQ là hình vuông

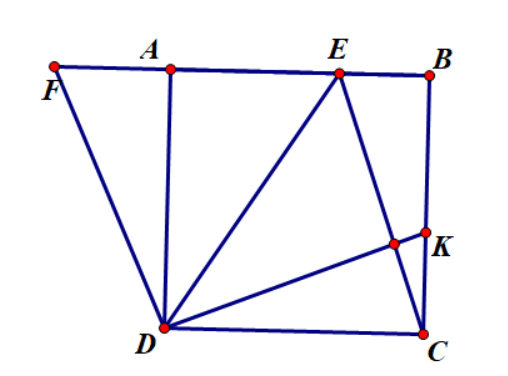
Ví dụ 3: Cho hình vuông ABCD, E thuộc AB. Phân giác \widehat {CDE}cắt BC tại K. Trên tia đối của tia AB, lấy F sao cho AF = CK. Chứng minh rằng:

a)  \Delta DEF cân

b) AE + CK = DE

Hướng dẫn giải

a) Xét \Delta ADFvà  \Delta CDKcó:

AF = CK

AD = CD

\Delta ADF = \Delta CDK \Rightarrow \left\{ \begin{array}{l} \widehat {DFA} = \widehat {CKD}\\ \widehat {ADF} = \widehat {CDK} \end{array} \right.

Ta có:\left\{ \begin{array}{l} \widehat {KDE} = \widehat {CDK}\\ \widehat {ADF} = \widehat {CDK} \end{array} \right. \Rightarrow \widehat {KDE} = \widehat {ADF} \Rightarrow \widehat {EDK} = \widehat {ADK}

Mà \widehat {ADK} = \widehat {CKD} \Rightarrow \widehat {EDF} = \widehat {CKD} \Rightarrow \widehat {EDF} = \widehat {EFD} \Rightarrow \Delta EDFcân tại E \Rightarrow DE = EF

Ta có: FE = AE + AF mà\left\{ \begin{array}{l} AF = \,CK\\ DE = EF \end{array} \right. \Rightarrow AE + CK = DE

Hi vọng Chuyên đề Chứng minh hình vuông là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 8 cũng như ôn luyện cho các kì thi sắp tới. Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 8, Lý thuyết Toán 8, Giải Toán 8, Luyện tập Toán 8, ... Chúc các bạn học tốt!

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 66
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần