Giaitoan.com Toán 9 Chuyên đề Toán 9 thi vào 10

Chứng minh 3 đường thẳng đồng quy ôn thi vào 10 Bài tập Toán 9

Nội dung
  • 3 Đánh giá

Chứng minh 3 đường thẳng đồng quy

Bài tập Toán 9: Chứng minh đồng quy là một dạng toán hình xuất hiện nhiều trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

1. Phương pháp chứng minh ba đường thẳng đồng quy

- Lợi dụng định lý về các đường đòng quy trong tam giác

+ Sử dụng định lý ba đường cao của tam giác đồng quy tại một điểm

+ Sử dụng định lý ba đường trung tuyến của tam giác đồng quy tại một điểm. Điểm đó được gọi là trọng tâm của tam giác

+ Sử dụng định lý: Ba đường phân giác của tam giác đồng quy tại một điểm

+ Giao điểm của hai đường phân giác ngoài nằm trên đường phân giác trong của góc thứ ba

- Sử dụng tính chất các đường chéo cắt nhau tại trung điểm mỗi đường của hình bình hành, hình chữ nhật, hình thoi, hình vuông.

- Lùi về quen thuôc, chứng minh ba điểm thẳng hàng hoặc giao điểm của hai đường nằm trên đường thẳng thứ ba

2. Bài tập chứng minh ba đường thẳng đồng quy

Ví dụ 1: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) đường kính MC, đường thẳng BM cắt đường tròn (O) tại D. Đường thẳng AD cắt đường tròn (O) tại S.

a) Chứng minh ABCD là tứ giác nội tiếp

b) Chứng minh CA là tia phân giác của góc SCB

c) Gọi E là giao điểm của Bc với đường tròn (O). Chứng minh các đường thẳng BA, EM, CD đồng quy

d) Chứng minh DM là phân giác góc ADE

e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE

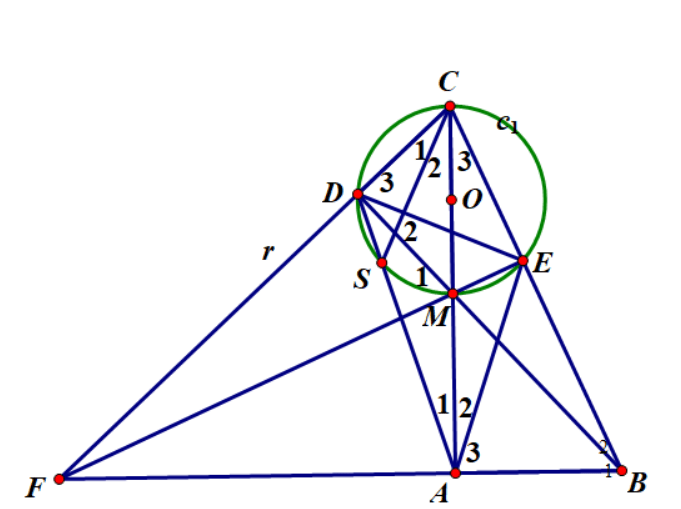
Hướng dẫn giải

a) Ta có \widehat {CAB} = {90^ \circ } ( tam giác ABC vuông tại A)

Lại có \widehat {MDC} = {90^ \circ }( Góc nội tiếp chắn nửa đường tròn) \Rightarrow \widehat {CDB} = 90

Nên A và D cùng nhìn BC dưới một góc bằng {90^ \circ }

ABCD là tứ giác nội tiếp

b) Ta có ABCD là tứ giác nội tiếp \Rightarrow \widehat {DSM} = \widehat {MCE} ( cùng chắn cung AB)

Mà \Rightarrow cung SM = cung ME = \Rightarrow \widehat {DCS} = \widehat {SCM}( hai góc nội tiếp đường tròn (O))

\RightarrowCA là tia phân giác của góc SCB

c) Xét \Delta CMB có BA \bot CM;CD \bot BM;ME \bot BC

F là trực tâm \Rightarrow BA, EM, CD đồng quy

d) Ta có cung SM = cung EM \ \Rightarrow \widehat {{D_1}} = \widehat {{D_2}} \Rightarrow DM là tia phân giác của góc ADE (1)
Ta có \widehat {MEC} = {90^ \circ }  ( góc nội tiếp chắn nửa đường tròn) \Rightarrow \widehat {MEB} = {90^ \circ }

Tứ giác AMEB có \widehat {MAB} = {90^ \circ };\widehat {MEB} = {90^ \circ } \Rightarrow \widehat {MAB} + \widehat {MEB} = {180^ \circ }

AMEB nội tiếp đường tròn \Rightarrow \widehat {{A_2}} = \widehat {{B_2}}

Tứ giác ABCD là tứ giác nội tiếp \Rightarrow \widehat {{A_1}} = \widehat {{B_2}}  ( nội tiếp cùng chắn cung CD)

\Rightarrow \widehat {{A_1}} = \widehat {{A_2}}  \Rightarrow AM là tia phân giác của DAE (2)

Từ (1) và (2) ta có M là tâm đường tròn nội tiếp tam giác ADE

Ví dụ 2: Cho tam giác ABC nội tiếp đường tròn (O; R). Tiếp tuyến tại B và C của đường tròn (O; R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A.

a) Chứng minh \Delta ABT đồng dạng \Delta BDT

b) Chứng minh AB. CD = BD. AC

c) Chứng minh rằng hai đường phân giác góc BAC; BDC và đường thẳng BC đồng quy tại một điểm

Hướng dẫn giải


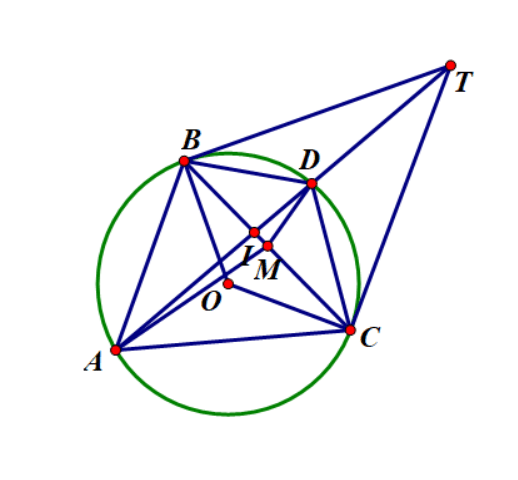
a) Xét \Delta ABT  và  \Delta BDT có:

\widehat {BTD}là góc chung

( cùng chắn cung BD)

\Delta ABT đồng dạng \Delta BDT (g- g)

b) Có \Delta ABT đồng dạng \Delta BDT \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{AT}}{{BT}}\,\,\left( 1 \right)

Chứng minh được \Delta ACT  đồng dạng  \Delta CDT   (g- g) \Rightarrow \dfrac{{AC}}{{CD}} = \dfrac{{AT}}{{CT}}\,\,\left( 2 \right)

Tiếp tuyến tại B và C cắt nhau tại T nên BT = CT (3)

Từ (1) (2) (3) có \dfrac{{AB}}{{BD}} = \dfrac{{AC}}{{CD}}\,\, \Rightarrow AB.CD = BD.AC

c) Phân giác góc BAC cắt BC tại I. Theo tính chất phân giác trong tam giác ta có: \dfrac{{IB}}{{IC}} = \dfrac{{AB}}{{AC}}

Từ AB. CD = BD. AC \Rightarrow \frac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}}\,\, \Rightarrow \dfrac{{IB}}{{IC}} = \dfrac{{BD}}{{CD}}\,\, \RightarrowDI là phân giác góc BDC

Do đó hai đường phân giác góc BAC và BDC và đường thẳng BC đồng quy

-----------------------------------

Hy vọng tài liệu Chứng minh đồng quy sẽ giúp ích cho các bạn học sinh học nắm chắc kiến thức chuyên đề Đường tròn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Ngoài ra mời quý thầy cô và học sinh tham khảo thêm một số nội dung:

Luyện tập Toán 9
Giải bài tập SGK Toán 9
Đề thi giữa học kì môn Toán 9

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 2.208
Tìm thêm: Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần