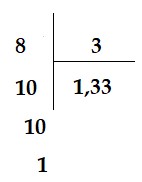Giaitoan.com Toán 5 Luyện tập Toán lớp 5

Các dạng toán về số thập phân lớp 5 Ôn tập về số thập phân

Nội dung Tải về
  • 57 Đánh giá

Toán lớp 5: Các bài toán về số thập phân

Toán lớp 5: Các dạng toán về số thập phân được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm nội dung lý thuyết kèm theo các ví dụ cụ thể và gợi ý cách giải các bài tập cụ thể về các dạng toán số thập phân thường gặp, giúp các em ôn tập, rèn luyện kỹ năng giải bài tập Toán lớp 5. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

1. Chuyển phân số thành số thập phân

+ Để chuyển phân số thành số thập phân, ta thực hiện việc chia tử số của phân số cho mẫu số của phân số đó.

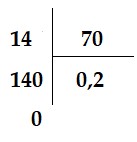
Ví dụ: Chuyển các phân số sau thành số thập phân: \frac{14}{70};\frac{8}{3}

Lời giải:

Thực hiện phép chia 14 : 70

Các dạng toán về số thập phân lớp 5

Vậy \frac{{14}}{{70}} = 0,2

Thực hiện phép chia 8 : 3

Các dạng toán về số thập phân lớp 5

Vậy \frac{8}{3} = 1,33

⁂ Chú ý: Nếu phép chia là phép chia có dư thì ta lấy đến chữ số thứ hai ở phần thập phân

+ Ngoài ra, với một số phân số, ta có thể đổi phân số thành phân số thập phân sau đó chuyển các phân số thập phân ấy thành số thập phân. Với các phân số có mẫu số là 10, 100, 1000, … thì số lượng số 0 của mẫu số tương ứng với số lượng số ở phần thập phân.

Ví dụ: Chuyển các phân số sau thành số thập phân: \frac{1}{2};\,\,\,\frac{5}{8}

Lời giải:

\frac{1}{2} = \frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}} = 0,5

\frac{5}{8} = \frac{{5 \times 125}}{{8 \times 125}} = \frac{{625}}{{1000}} = 0,625

2. Chuyển hỗn số thành số thập phân

Để chuyển hỗn số thành số thập phân, ta có hai cách sau:

• Cách 1: Chuyển hỗn số thành phân số sau đó thực hiện chuyển phân số thành số thập phân.

• Cách 2: Giữ nguyên phần nguyên, chuyển phần phân số thành số thập phân sau đó cộng với phần nguyên.

Ví dụ 1: Chuyển hỗn số 3\frac{2}{5} thành số thập phân

Lời giải:

3\frac{2}{5} = \frac{{3 \times 5 + 2}}{5} = \frac{{17}}{5} = \frac{{17 \times 2}}{{5 \times 2}} = \frac{{34}}{{10}} = 3,4

Ví dụ 2: Chuyển hỗn số 7\frac{5}{8} thành số thập phân

Lời giải:

7\frac{5}{8} = 7 + \frac{5}{8} = 7 + \frac{{5 \times 125}}{{8 \times 125}} = 7 + \frac{{625}}{{1000}} = 7 + 0,625 = 7,625

3. Chuyển các đơn vị đo độ dài, đo khối lượng thành số thập phân

Để chuyển các đơn vị đo độ dài, đo khối lượng thành số thập phân, ta thực hiện các bước sau:

• Xác định hai đơn vị đo độ dài đã cho và tìm mối liên hệ giữa các đơn vị đo ấy.

• Viết số đo độ dài đã cho thành phân số thập phân.

• Chuyển phân số thập phân thành số thập phân.

Ví dụ: Điền số thập phân thích hợp vào chỗ chấm: 5 m 14 cm = ...m

Lời giải:

Có 1 m = 100 cm hay 1 cm = \frac{1}{{100}} m nên 14 cm = \frac{{14}}{{100}} m = 0,14 m

Vậy 5 m 14 cm = 5,14 m

4. Chuyển số thập phân thành phân số thập phân

Để đổi một số thập phân thành phân số thập phân ta làm như sau:

• Bước 1: Xác định số chữ số ở phần thập phân

• Bước 2: Viết mẫu số của phần số là các số 10, 100, 1000, … với số chữ số 0 bằng số chữ số ở phần thập phân xác định ở bước 1.

Ví dụ: Chuyển số thập phân 6,423 thành phân số thập phân.

Lời giải:

• Bước 1: Số chữ số ở phần thập phân là 3 chữ số → Phân số thập phân có mẫu số bằng 1000.

• Bước 2: Viết phân số: 6,423 = \frac{{6423}}{{1000}}

5. So sánh số thập phân

• So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

• Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

• Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

Ví dụ: Viết các số thập phân dưới đây theo thứ tự từ bé đến lớn:

6,37; 5,18; 6,29; 5,7

Lời giải:

So sánh phần nguyên của các số đã cho ta có 5 < 6.

So sánh hai số có cùng phần nguyên, ta được: 6,37 > 6,29 và 5,18 < 5,7

Vậy sắp xếp các số theo thứ tự từ bé đến lớn được:

5,18; 5,7; 6,29; 6,37

6. Làm tròn số thập phân

a) Làm tròn số thập phân đến số tự nhiên gần nhất.

Khi làm tròn số thập phân đến số tự nhiên gần nhất, ta so sánh chữ số ở hàng phần mười với 5. Nếu chữ số hàng phần mười bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.

Ví dụ:

b) Làm tròn số thập phân đến hàng phần mười, hàng phần trăm.

• Khi làm tròn số thập phân đến hàng phần mười, ta so sánh chữ số hàng phần trăm với 5. Nếu chữ số hàng phần trăm bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.

• Khi làm tròn số thập phân đến hàng phần trăm, ta so sánh chữ số hàng phần nghìn với 5. Nếu chữ số hàng phần nghìn bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.

Ví dụ:

Bài tập tự luyện các dạng Toán về số thập phân

Bài 1: Chuyển các phân số sau thành số thập phân:

\frac{{28}}{{140}};\,\,\,\frac{{33}}{{75}};\,\,\,\frac{{216}}{{900}};\,\,\,\frac{{415}}{{1250}}

Bài 2: Chuyển các hỗn số dưới đây thành số thập phân:

2\frac{{23}}{{75}};\,\,5\,\frac{{28}}{{140}};\,\,\,4\frac{{216}}{{900}};\,\,\,1\frac{{415}}{{1250}}

Bài 3: Điền số thập phân thích hợp vào chỗ chấm:

a) 156 cm = ... mb) 508 cm = ... m
c) 2 765 m = ... kmd) 9 087 m = ... km
e) 3 tấn 218 kg = ..... tấng) 4 tấn 6 kg = .....tấn
h) 17 tấn 605 kg = .....tấni) 10 tấn 15 kg = .....tấn
k) 22 mm2 = ...... cm2l)

Bài 4: Chuyển các số thập phân dưới đây thành phân số thập phân:

2,25; 7,5; 0,6; 0,55; 0,004; 0,01; 1,7; 2; 0,36; 0,19

Bài 5: 

a) Xếp theo thứ tự từ bé đến lớn các số sau đây:

45,738; 44,835; 45,728; 44,815; 43,995.

b) Xếp theo thứ tự từ lớn đến bé các số sau đây:

26,18; 30,75; 38,08; 39,80; 37,7.

Bài 6: Làm tròn số thập phân gồm "Một nghìn đơn vị, bảy mươi mốt phần nghìn" đến hàng phần trăm.

Bài 7: Làm tròn một số thập phân đến hàng phần nghìn, ta được số 85,745. Tìm số thập phân đó.

Bài 8: Viết số thập phân nhỏ nhất có các chữ số khác nhau mà tổng các chữ số của số đó bằng 12.

Bài tập trắc nghiệm các dạng Toán về số thập phân

Câu 1: Viết phân số \frac{35}{100} về dạng số thập phân được kết quả là:

A. 35B. 3,5C. 0,35D. 0,035

Câu 2: Viết số 0,008 dưới dạng phân số thập phân được kết quả là:

A. \frac{8}{1000}B. \frac{8}{100}C. \frac{8}{10}D. \frac{8}{1}

Câu 3: Dấu so sánh thích hợp để điền vào chỗ chấm 3,154 ... 3,054 là:

A. =B. <C. >D. Không có dấu so sánh thích hợp

Câu 4: Viết các phân số sau dưới dạng số thập phân được kết quả là:

\frac{2}{10};\frac{16}{1000}; \frac{252}{100}; \frac{1938}{100}

A. 2,0; 16,000; 252,00; 1938,00

B. 0,2; 0,16; 0,252; 0,1938

C. 2,0; 1,6; 2,52; 1,938

D. 0,2; 0,016; 2,52; 19,38

Câu 5: Sắp xếp các số thập phân sau theo thứ tự từ bé đến lớn:

2,52; 16,74; 3,33; 1,28

A. 3,33 < 1,28 < 2,52 < 16,74

B. 1,28 < 2,52 < 3,33 < 16,74

C. 2,52 < 3,33 < 1,28 < 16,74

D. 16,74 < 1,28 < 2,52 < 3,33

Câu 6: Sắp xếp các số thập phân sau theo thứ tự từ lớn đến bé:

15,37; 15,49; 15,13; 15,08

A. 15,49 > 15,37 > 15,08 > 15,13

B. 15,08 > 15,37 > 15,13 > 15,49

C. 15,49 > 15,37 > 15,13 > 15,08

D. 15,13 > 15,08 > 15,37 > 15,49

Câu 7: Trong một cuộc thi chạy 600m nam, có bốn vận động viên đạt thành tích cao nhất là Nam: 50,15 giây; Dũng: 51,12 giây; Hùng: 52,18 giây và Minh: 49,2 giây. Các vận động viên đã về Nhất, Nhì, Ba, Tư lần lượt là:

A. Minh, Dũng, Nam, Hùng

B. Minh, Nam, Dũng, Hùng

C. Dũng, Minh, Nam, Hùng

D. Hùng, Dũng, Nam, Minh

Câu 8: Trong các số sau, số nào lớn nhất?

A. 48,457

B. 4,8457

C. 484,57

D. 4845,7

Câu 9: Chữ số thích hợp điền vào chỗ trống là: 9_83 < 9 183

A. 0

B. 1

C. 2

D. 3

Câu 10:  Hóa đơn tiền nước của nhà cô Hồng là 256,910 nghìn đồng. Làm tròn số tiền đó đến hàng đơn vị thì số tiền nước nhà cô Hồng là:

-------------------------

  • 39.140 lượt xem
Chia sẻ bởi: Bọ Cạp
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán lớp 5 Bài tập Toán lớp 5
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Xem thêm bài viết khác

    Xem thêm Luyện tập Toán lớp 5

    Chủ đề liên quan

    Luyện tập Toán lớp 5